scipy.interpolate.RectSphereBivariateSpline.

ev

RectSphereBivariateSpline.ev(theta, phi, dtheta=0, dphi=0)

Evaluieren des Splines an Punkten

Gibt den interpolierten Wert an (theta[i], phi[i]), i=0,...,len(theta)-1 zurück.

Parameter:

theta, phiarray_like

Eingabekoordinaten. Standardmäßiges Numpy-Broadcasting wird beachtet. Die Reihenfolge der Achsen ist konsistent mit np.meshgrid(…, indexing=”ij”) und inkonsistent mit der Standardreihenfolge np.meshgrid(…, indexing=”xy”).

dthetaint, optional

Ordnung der Theta-Ableitung

Hinzugefügt in Version 0.14.0.

dphiint, optional

Ordnung der Phi-Ableitung

Hinzugefügt in Version 0.14.0.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Angenommen, wir möchten Splines verwenden, um eine bivariate Funktion auf einer Kugel zu interpolieren. Der Wert der Funktion ist auf einem Gitter von Längen- und Kolatituden bekannt.

>>> import numpy as np
>>> from scipy.interpolate import RectSphereBivariateSpline
>>> def f(theta, phi):
...     return np.sin(theta) * np.cos(phi)

Wir werten die Funktion auf dem Gitter aus. Beachten Sie, dass die Standard-Indexing=”xy” von meshgrid nach der Interpolation ein unerwartetes (transponiertes) Ergebnis liefern würde.

>>> thetaarr = np.linspace(0, np.pi, 22)[1:-1]
>>> phiarr = np.linspace(0, 2 * np.pi, 21)[:-1]
>>> thetagrid, phigrid = np.meshgrid(thetaarr, phiarr, indexing="ij")
>>> zdata = f(thetagrid, phigrid)

Wir richten anschließend den Interpolator ein und verwenden ihn, um die Funktion an Punkten auszuwerten, die nicht auf dem ursprünglichen Gitter liegen.

>>> rsbs = RectSphereBivariateSpline(thetaarr, phiarr, zdata)
>>> thetainterp = np.linspace(thetaarr[0], thetaarr[-1], 200)
>>> phiinterp = np.linspace(phiarr[0], phiarr[-1], 200)
>>> zinterp = rsbs.ev(thetainterp, phiinterp)

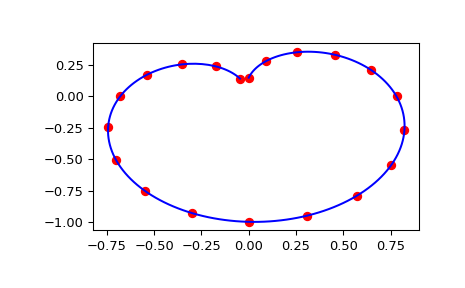
Schließlich plotten wir die Originaldaten für einen diagonalen Schnitt durch das ursprüngliche Gitter und die Spline-Approximation entlang desselben Schnitts.

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(1, 1, 1)
>>> ax1.plot(np.sin(thetaarr) * np.sin(phiarr), np.diag(zdata), "or")
>>> ax1.plot(np.sin(thetainterp) * np.sin(phiinterp), zinterp, "-b")
>>> plt.show()

ZurückIn Tab öffnen