scipy.interpolate.

RectSphereBivariateSpline

class scipy.interpolate.RectSphereBivariateSpline(u, v, r, s=0.0, pole_continuity=False, pole_values=None, pole_exact=False, pole_flat=False)

Bivariate Spline-Approximation über ein rechteckiges Gitter auf einer Sphäre.

Kann zur Glättung von Daten verwendet werden.

Hinzugefügt in Version 0.11.0.

Parameter:

uarray_like

1-D-Array von Kolatitudenkoordinaten in streng aufsteigender Reihenfolge. Koordinaten müssen in Radiant angegeben werden und im offenen Intervall (0, pi) liegen.

varray_like

1-D-Array von Längengradkoordinaten in streng aufsteigender Reihenfolge. Koordinaten müssen in Radiant angegeben werden. Das erste Element (v[0]) muss im Intervall [-pi, pi) liegen. Das letzte Element (v[-1]) muss v[-1] <= v[0] + 2*pi erfüllen.

rarray_like

2-D-Array von Daten mit der Form (u.size, v.size).

sfloat, optional

Positiver Glättungsfaktor, der für die Schätzbedingung definiert ist (s=0 bedeutet Interpolation).

pole_continuitybool oder (bool, bool), optional

Ordnung der Stetigkeit an den Polen u=0 (pole_continuity[0]) und u=pi (pole_continuity[1]). Die Ordnung der Stetigkeit am Pol ist 1 oder 0, wenn dieser True oder False ist, entsprechend. Standard ist False.

pole_valuesfloat oder (float, float), optional

Datenwerte an den Polen u=0 und u=pi. Entweder der gesamte Parameter oder jedes einzelne Element kann None sein. Standard ist None.

pole_exactbool oder (bool, bool), optional

Exaktheit des Datenwerts an den Polen u=0 und u=pi. Wenn True, wird der Wert als der korrekte Funktionswert betrachtet und exakt angepasst. Wenn False, wird der Wert wie andere Datenwerte behandelt. Standard ist False.

pole_flatbool oder (bool, bool), optional

Für die Pole bei u=0 und u=pi, geben Sie an, ob die Approximation verschwindende Ableitungen hat. Standard ist False.

Methoden

__call__(theta, phi[, dtheta, dphi, grid])	Evaluieren des Splines oder seiner Ableitungen an gegebenen Positionen.
ev(theta, phi[, dtheta, dphi])	Evaluieren des Splines an Punkten
get_coeffs()	Gib die Spline-Koeffizienten zurück.
get_knots()	Gibt ein Tupel (tx,ty) zurück, wobei tx,ty die Knotenpositionen des Splines bezüglich der x- und y-Variablen enthalten.
get_residual()	Gibt die gewichtete Summe der quadrierten Residuen der Spline-Approximation zurück: sum ((w[i]*(z[i]-s(x[i],y[i])))**2,axis=0)
partial_derivative(dx, dy)	Konstruiert einen neuen Spline, der eine partielle Ableitung dieses Splines darstellt.

Siehe auch

BivariateSpline

Eine Basisklasse für bivariate Splines.

UnivariateSpline

Ein geglätteter univariater Spline zur Anpassung an eine gegebene Menge von Datenpunkten.

SmoothBivariateSpline

Ein glättender bivariate Spline durch die gegebenen Punkte

LSQBivariateSpline

Ein bivariate Spline unter Verwendung von gewichteter Kleinster-Quadrate-Anpassung

SmoothSphereBivariateSpline

Ein glättender bivariate Spline in Kugelkoordinaten

LSQSphereBivariateSpline

Ein bivariate Spline in Kugelkoordinaten unter Verwendung von gewichteter Kleinster-Quadrate-Anpassung

RectBivariateSpline

ein bivariate Spline über ein rechteckiges Gitter.

bisplrep

Eine Funktion zum Finden einer B-Spline-Darstellung einer Oberfläche im Bivariaten

bisplev

Eine Funktion zur Auswertung eines B-Splines im Bivariaten und seiner Ableitungen

Hinweise

Derzeit wird nur die Glättungs-Spline-Approximation unterstützt (iopt[0] = 0 und iopt[0] = 1 in der FITPACK-Routine). Die exakte Least-Squares-Spline-Approximation ist noch nicht implementiert.

Bei der tatsächlichen Durchführung der Interpolation müssen die angeforderten v-Werte innerhalb desselben Intervalls der Länge 2pi liegen, aus dem die ursprünglichen v-Werte ausgewählt wurden.

Weitere Informationen finden Sie auf der FITPACK-Website zu dieser Funktion.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Angenommen, wir haben globale Daten auf einem groben Gitter

>>> import numpy as np
>>> lats = np.linspace(10, 170, 9) * np.pi / 180.
>>> lons = np.linspace(0, 350, 18) * np.pi / 180.
>>> data = np.dot(np.atleast_2d(90. - np.linspace(-80., 80., 18)).T,
...               np.atleast_2d(180. - np.abs(np.linspace(0., 350., 9)))).T

Wir möchten sie auf ein globales Ein-Grad-Gitter interpolieren

>>> new_lats = np.linspace(1, 180, 180) * np.pi / 180
>>> new_lons = np.linspace(1, 360, 360) * np.pi / 180
>>> new_lats, new_lons = np.meshgrid(new_lats, new_lons)

Wir müssen das Interpolatorobjekt einrichten

>>> from scipy.interpolate import RectSphereBivariateSpline
>>> lut = RectSphereBivariateSpline(lats, lons, data)

Schließlich interpolieren wir die Daten. Das RectSphereBivariateSpline-Objekt akzeptiert nur 1-D-Arrays als Eingabe, daher müssen wir einige Reshapings vornehmen.

>>> data_interp = lut.ev(new_lats.ravel(),
...                      new_lons.ravel()).reshape((360, 180)).T

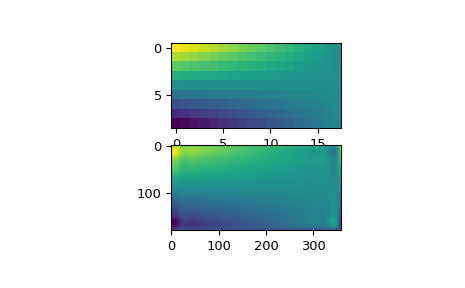
Wenn man die Originaldaten und die interpolierten Daten betrachtet, kann man sehen, dass der Interpolator die Originaldaten sehr gut reproduziert

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(211)
>>> ax1.imshow(data, interpolation='nearest')
>>> ax2 = fig.add_subplot(212)
>>> ax2.imshow(data_interp, interpolation='nearest')
>>> plt.show()

Die Wahl des optimalen Wertes für s kann eine heikle Aufgabe sein. Empfohlene Werte für s hängen von der Genauigkeit der Datenwerte ab. Wenn der Benutzer eine Vorstellung von den statistischen Fehlern in den Daten hat, kann er auch eine geeignete Schätzung für s finden. Indem er davon ausgeht, dass der Interpolator bei Angabe des richtigen s eine Spline f(u,v) verwendet, die die der Daten zugrundeliegende Funktion exakt reproduziert, kann er sum((r(i,j)-s(u(i),v(j)))**2) auswerten, um eine gute Schätzung für dieses s zu finden. Wenn sie beispielsweise weiß, dass die statistischen Fehler in ihren r(i,j)-Werten nicht größer als 0,1 sind, kann sie erwarten, dass ein gutes s einen Wert von nicht mehr als u.size * v.size * (0.1)**2 hat.

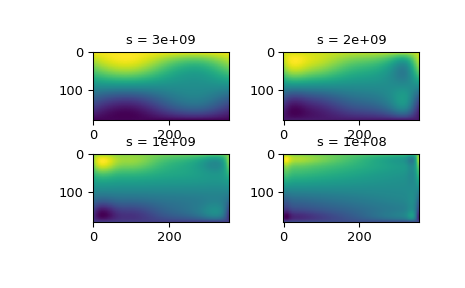
Wenn nichts über den statistischen Fehler in r(i,j) bekannt ist, muss s durch Versuch und Irrtum ermittelt werden. Am besten ist es, mit einem sehr großen Wert für s zu beginnen (um das Least-Squares-Polynom und die entsprechende Obergrenze fp0 für s zu bestimmen) und dann den Wert von s schrittweise zu verringern (z. B. zunächst um den Faktor 10, d.h. s = fp0 / 10, fp0 / 100, ... und genauer, wenn die Approximation mehr Details zeigt), um engere Anpassungen zu erhalten.

Die Interpolationsergebnisse für verschiedene Werte von s geben Einblick in diesen Prozess

>>> fig2 = plt.figure()
>>> s = [3e9, 2e9, 1e9, 1e8]
>>> for idx, sval in enumerate(s, 1):
...     lut = RectSphereBivariateSpline(lats, lons, data, s=sval)
...     data_interp = lut.ev(new_lats.ravel(),
...                          new_lons.ravel()).reshape((360, 180)).T
...     ax = fig2.add_subplot(2, 2, idx)
...     ax.imshow(data_interp, interpolation='nearest')
...     ax.set_title(f"s = {sval:g}")
>>> plt.show()

ZurückIn Tab öffnen