SmoothSphereBivariateSpline#
- class scipy.interpolate.SmoothSphereBivariateSpline(theta, phi, r, w=None, s=0.0, eps=1e-16)[Quelle]#
Geglättete bivariate Spline-Approximation in Kugelkoordinaten.
Hinzugefügt in Version 0.11.0.
- Parameter:
- theta, phi, rarray_like
1-D-Sequenzen von Datenpunkten (Reihenfolge ist nicht wichtig). Koordinaten müssen in Radiant angegeben werden. Theta muss im Intervall
[0, pi]liegen, und phi muss im Intervall[0, 2pi]liegen.- warray_like, optional
Positive 1-D-Sequenz von Gewichten.
- sfloat, optional
Positiver Glättungsfaktor, definiert für die Schätzbedingung:
sum((w(i)*(r(i) - s(theta(i), phi(i))))**2, axis=0) <= sStandardmäßigs=len(w), was ein guter Wert sein sollte, wenn1/w[i]eine Schätzung der Standardabweichung vonr[i]ist.- epsfloat, optional
Ein Schwellenwert zur Bestimmung des effektiven Rangs eines überbestimmten linearen Gleichungssystems. eps sollte einen Wert im offenen Intervall
(0, 1)haben, der Standardwert ist 1e-16.
Methoden
__call__(theta, phi[, dtheta, dphi, grid])Evaluieren des Splines oder seiner Ableitungen an gegebenen Positionen.
ev(theta, phi[, dtheta, dphi])Evaluieren des Splines an Punkten
Gib die Spline-Koeffizienten zurück.
Gibt ein Tupel (tx,ty) zurück, wobei tx,ty die Knotenpositionen des Splines bezüglich der x- und y-Variablen enthalten.
Gibt die gewichtete Summe der quadrierten Residuen der Spline-Approximation zurück: sum ((w[i]*(z[i]-s(x[i],y[i])))**2,axis=0)
partial_derivative(dx, dy)Konstruiert einen neuen Spline, der eine partielle Ableitung dieses Splines darstellt.
Siehe auch
BivariateSplineEine Basisklasse für bivariate Splines.
UnivariateSplineEin geglätteter univariater Spline zur Anpassung an eine gegebene Menge von Datenpunkten.
SmoothBivariateSplineEin glättender bivariate Spline durch die gegebenen Punkte
LSQBivariateSplineEin bivariate Spline unter Verwendung von gewichteter Kleinster-Quadrate-Anpassung
RectSphereBivariateSplineEin bivariate Spline über ein rechteckiges Gitter auf einer Kugel
LSQSphereBivariateSplineEin bivariate Spline in Kugelkoordinaten unter Verwendung von gewichteter Kleinster-Quadrate-Anpassung
RectBivariateSplineein bivariate Spline über ein rechteckiges Gitter.
bisplrepEine Funktion zum Finden einer B-Spline-Darstellung einer Oberfläche im Bivariaten
bisplevEine Funktion zur Auswertung eines B-Splines im Bivariaten und seiner Ableitungen
Hinweise
Weitere Informationen finden Sie auf der FITPACK-Website zu dieser Funktion.
Beispiele
Angenommen, wir haben globale Daten auf einem groben Gitter (die Eingabedaten müssen nicht auf einem Gitter liegen)
>>> import numpy as np >>> theta = np.linspace(0., np.pi, 7) >>> phi = np.linspace(0., 2*np.pi, 9) >>> data = np.empty((theta.shape[0], phi.shape[0])) >>> data[:,0], data[0,:], data[-1,:] = 0., 0., 0. >>> data[1:-1,1], data[1:-1,-1] = 1., 1. >>> data[1,1:-1], data[-2,1:-1] = 1., 1. >>> data[2:-2,2], data[2:-2,-2] = 2., 2. >>> data[2,2:-2], data[-3,2:-2] = 2., 2. >>> data[3,3:-2] = 3. >>> data = np.roll(data, 4, 1)
Wir müssen das Interpolatorobjekt einrichten
>>> lats, lons = np.meshgrid(theta, phi) >>> from scipy.interpolate import SmoothSphereBivariateSpline >>> lut = SmoothSphereBivariateSpline(lats.ravel(), lons.ravel(), ... data.T.ravel(), s=3.5)
Als erster Test sehen wir uns an, was der Algorithmus zurückgibt, wenn er auf die Eingabekoordinaten angewendet wird
>>> data_orig = lut(theta, phi)
Schließlich interpolieren wir die Daten auf ein feineres Gitter
>>> fine_lats = np.linspace(0., np.pi, 70) >>> fine_lons = np.linspace(0., 2 * np.pi, 90)
>>> data_smth = lut(fine_lats, fine_lons)
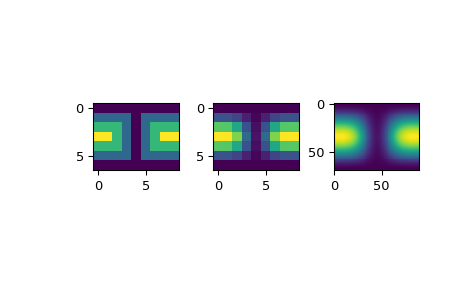
>>> import matplotlib.pyplot as plt >>> fig = plt.figure() >>> ax1 = fig.add_subplot(131) >>> ax1.imshow(data, interpolation='nearest') >>> ax2 = fig.add_subplot(132) >>> ax2.imshow(data_orig, interpolation='nearest') >>> ax3 = fig.add_subplot(133) >>> ax3.imshow(data_smth, interpolation='nearest') >>> plt.show()