approximate_taylor_polynomial#
- scipy.interpolate.approximate_taylor_polynomial(f, x, degree, scale, order=None)[Quelle]#
Schätzt das Taylor-Polynom von f an der Stelle x durch Polynomanpassung.
- Parameter:
- faufrufbar
Die Funktion, deren Taylor-Polynom gesucht wird. Sollte einen Vektor von x-Werten akzeptieren.
- xSkalar
Der Punkt, an dem das Polynom ausgewertet werden soll.
- degreeint
Der Grad des Taylor-Polynoms
- scaleSkalar
Die Breite des Intervalls, das zur Auswertung des Taylor-Polynoms verwendet wird. Funktionswerte, die sich über diesen Bereich erstrecken, werden zur Anpassung des Polynoms verwendet. Muss sorgfältig gewählt werden.
- orderint oder None, optional
Die Ordnung des Polynoms, das für die Anpassung verwendet wird; f wird
order+1Mal ausgewertet. Wenn None, wird degree verwendet.
- Rückgabe:
- ppoly1d-Instanz
Das Taylor-Polynom (verschoben zum Ursprung, so dass z.B. p(0)=f(x)).
Hinweise
Die geeignete Wahl von „scale“ ist ein Kompromiss; zu groß und die Funktion unterscheidet sich zu sehr von ihrem Taylor-Polynom, um ein gutes Ergebnis zu erzielen, zu klein und Rundungsfehler überwältigen die Terme höherer Ordnung. Der verwendete Algorithmus wird um Ordnung 30 herum auch unter idealen Umständen numerisch instabil.
Die Wahl von order etwas größer als degree kann die Terme höherer Ordnung verbessern.
Beispiele
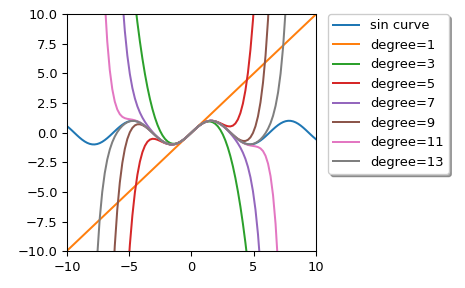
Wir können Taylor-Approximationspolynome der Sinusfunktion mit verschiedenen Graden berechnen
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.interpolate import approximate_taylor_polynomial >>> x = np.linspace(-10.0, 10.0, num=100) >>> plt.plot(x, np.sin(x), label="sin curve") >>> for degree in np.arange(1, 15, step=2): ... sin_taylor = approximate_taylor_polynomial(np.sin, 0, degree, 1, ... order=degree + 2) ... plt.plot(x, sin_taylor(x), label=f"degree={degree}") >>> plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', ... borderaxespad=0.0, shadow=True) >>> plt.tight_layout() >>> plt.axis([-10, 10, -10, 10]) >>> plt.show()