lagrange#
- scipy.interpolate.lagrange(x, w)[Quelle]#
Gibt ein Lagrange-Interpolationspolynom zurück.
Gegeben zwei 1-D-Arrays x und w, gibt das Lagrange-Interpolationspolynom durch die Punkte
(x, w)zurück.Warnung: Diese Implementierung ist numerisch instabil. Erwarten Sie nicht, mehr als etwa 20 Punkte verwenden zu können, selbst wenn diese optimal gewählt sind.
- Parameter:
- xarray_like
x repräsentiert die x-Koordinaten einer Menge von Datenpunkten.
- warray_like
w repräsentiert die y-Koordinaten einer Menge von Datenpunkten, d. h. f(x).
- Rückgabe:
- lagrange
numpy.poly1dInstanz Das Lagrange-Interpolationspolynom.
- lagrange
Hinweise
Der Name dieser Funktion bezieht sich auf die Tatsache, dass das zurückgegebene Objekt ein Lagrange-Polynom darstellt, das eindeutige Polynom niedrigsten Grades, das eine gegebene Menge von Daten interpoliert [1]. Es berechnet das Polynom mithilfe der Formel für Newtonsche dividierte Differenzen [2]; das heißt, es arbeitet mit Newtonschen Basispoylnomen anstelle von Lagrange-Basispoylnomen. Für numerische Berechnungen ist die baryzentrische Form der Lagrange-Interpolation (
scipy.interpolate.BarycentricInterpolator) typischerweise besser geeignet.Referenzen
[1]Lagrange-Polynom. Wikipedia. https://en.wikipedia.org/wiki/Lagrange_polynomial
[2]Newton-Polynom. Wikipedia. https://en.wikipedia.org/wiki/Newton_polynomial
Beispiele
Interpoliere \(f(x) = x^3\) mit 3 Punkten.
>>> import numpy as np >>> from scipy.interpolate import lagrange >>> x = np.array([0, 1, 2]) >>> y = x**3 >>> poly = lagrange(x, y)
Da es nur 3 Punkte gibt, hat das Lagrange-Polynom den Grad 2. Explizit ist es gegeben durch
\[\begin{split}\begin{aligned} L(x) &= 1\times \frac{x (x - 2)}{-1} + 8\times \frac{x (x-1)}{2} \\ &= x (-2 + 3x) \end{aligned}\end{split}\]>>> from numpy.polynomial.polynomial import Polynomial >>> Polynomial(poly.coef[::-1]).coef array([ 0., -2., 3.])
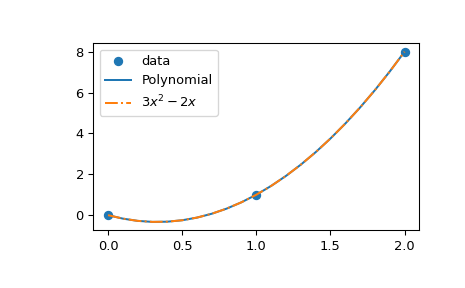
>>> import matplotlib.pyplot as plt >>> x_new = np.arange(0, 2.1, 0.1) >>> plt.scatter(x, y, label='data') >>> plt.plot(x_new, Polynomial(poly.coef[::-1])(x_new), label='Polynomial') >>> plt.plot(x_new, 3*x_new**2 - 2*x_new + 0*x_new, ... label=r"$3 x^2 - 2 x$", linestyle='-.') >>> plt.legend() >>> plt.show()