scipy.interpolate.

make_interp_spline#

scipy.interpolate.make_interp_spline(x, y, k=3, t=None, bc_type=None, axis=0, check_finite=True)[Quelle]#

Erstellt eine interpolierende B-Spline mit vorgegebenem Grad und Randbedingungen.

Parameter:

xarray_like, Form (n,)

Abszissen.

yarray_like, Form (n, …)

Ordinaten.

kint, optional

B-Spline-Grad. Standard ist kubisch, k = 3.

tarray_like, Form (nt + k + 1,), optional.

Knoten. Die Anzahl der Knoten muss mit der Anzahl der Datenpunkte und der Anzahl der Ableitungen an den Rändern übereinstimmen. Insbesondere muss nt - n gleich len(deriv_l) + len(deriv_r) sein.

bc_type2-Tupel oder None

Randbedingungen. Standard ist None, was bedeutet, dass die Randbedingungen automatisch gewählt werden. Andernfalls muss es sich um ein Tupel der Länge zwei handeln, bei dem das erste Element (deriv_l) die Randbedingungen bei x[0] festlegt und das zweite Element (deriv_r) die Randbedingungen bei x[-1] festlegt. Jedes davon muss ein Iterable von Paaren (order, value) sein, das die Werte der Ableitungen bestimmter Ordnungen an den gegebenen Rändern des Interpolationsintervalls angibt. Alternativ werden die folgenden String-Aliase erkannt

"clamped": Die ersten Ableitungen an den Enden sind Null. Dies ist
äquivalent zu bc_type=([(1, 0.0)], [(1, 0.0)]).
"natural": Die zweiten Ableitungen an den Enden sind Null. Dies ist äquivalent zu bc_type=([(2, 0.0)], [(2, 0.0)]).
"not-a-knot" (Standard): Die ersten und zweiten Segmente sind dasselbe Polynom. Dies ist äquivalent zu bc_type=None.
"periodic": Die Werte und die ersten k-1 Ableitungen an den Enden sind äquivalent.

axisint, optional

Interpolationsachse. Standard ist 0.

check_finitebool, optional

Ob geprüft werden soll, ob die Eingabearrays nur endliche Zahlen enthalten. Deaktivierung kann zu Leistungsgewinnen führen, aber auch zu Problemen (Abstürze, Nicht-Terminierung) führen, wenn die Eingaben Unendlichkeiten oder NaNs enthalten. Standard ist True.

Rückgabe:

bBSpline-Objekt: Ein BSpline-Objekt vom Grad k und mit Knoten t.

Siehe auch

BSpline: Basisklasse, die die B-Spline-Objekte darstellt
CubicSpline: eine kubische Spline in der Polynombasis
make_lsq_spline: eine ähnliche Factory-Funktion für Spline-Fitting
UnivariateSpline: ein Wrapper über FITPACK-Spline-Fitting-Routinen
splrep: ein Wrapper über FITPACK-Spline-Fitting-Routinen

Beispiele

Verwendet kubische Interpolation auf Chebyshev-Knoten

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> def cheb_nodes(N):
...     jj = 2.*np.arange(N) + 1
...     x = np.cos(np.pi * jj / 2 / N)[::-1]
...     return x

>>> x = cheb_nodes(20)
>>> y = np.sqrt(1 - x**2)

>>> from scipy.interpolate import BSpline, make_interp_spline
>>> b = make_interp_spline(x, y)
>>> np.allclose(b(x), y)
True

Beachten Sie, dass der Standard eine kubische Spline mit einer "not-a-knot"-Randbedingung ist

>>> b.k
3

Hier verwenden wir eine „natürliche“ Spline mit Null-Zweitableitungen an den Rändern

>>> l, r = [(2, 0.0)], [(2, 0.0)]
>>> b_n = make_interp_spline(x, y, bc_type=(l, r))  # or, bc_type="natural"
>>> np.allclose(b_n(x), y)
True
>>> x0, x1 = x[0], x[-1]
>>> np.allclose([b_n(x0, 2), b_n(x1, 2)], [0, 0])
True

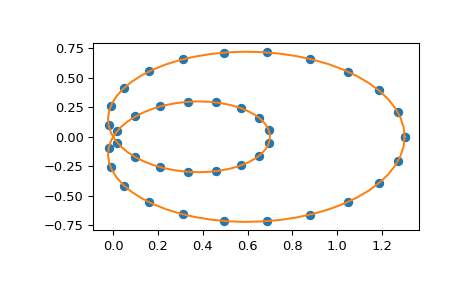
Interpolation von parametrischen Kurven wird ebenfalls unterstützt. Als Beispiel berechnen wir eine Diskretisierung einer Schneckenkurve in Polarkoordinaten

>>> phi = np.linspace(0, 2.*np.pi, 40)
>>> r = 0.3 + np.cos(phi)
>>> x, y = r*np.cos(phi), r*np.sin(phi)  # convert to Cartesian coordinates

Erstellt eine interpolierende Kurve, die durch den Winkel parametrisiert wird

>>> spl = make_interp_spline(phi, np.c_[x, y])

Evaluiert den Interpolanten auf einem feineren Gitter (beachten Sie, dass wir das Ergebnis transponieren, um es in ein Paar von x- und y-Arrays zu entpacken)

>>> phi_new = np.linspace(0, 2.*np.pi, 100)
>>> x_new, y_new = spl(phi_new).T

Zeichnet das Ergebnis

>>> plt.plot(x, y, 'o')
>>> plt.plot(x_new, y_new, '-')
>>> plt.show()

../../_images/scipy-interpolate-make_interp_spline-1_00_00.png

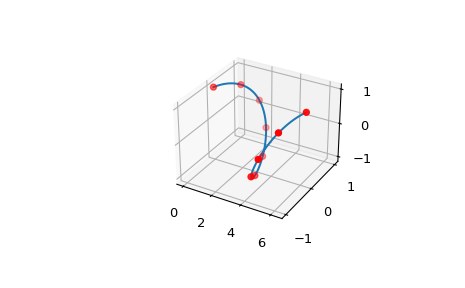
Erstellt eine B-Spline-Kurve mit 2-dimensionalem y

>>> x = np.linspace(0, 2*np.pi, 10)
>>> y = np.array([np.sin(x), np.cos(x)])

Die periodische Bedingung ist erfüllt, da die y-Koordinaten der Punkte an den Enden äquivalent sind

>>> ax = plt.axes(projection='3d')
>>> xx = np.linspace(0, 2*np.pi, 100)
>>> bspl = make_interp_spline(x, y, k=5, bc_type='periodic', axis=1)
>>> ax.plot3D(xx, *bspl(xx))
>>> ax.scatter3D(x, *y, color='red')
>>> plt.show()

../../_images/scipy-interpolate-make_interp_spline-1_01_00.png