scipy.interpolate.

make_lsq_spline#

scipy.interpolate.make_lsq_spline(x, y, t, k=3, w=None, axis=0, check_finite=True, *, method='qr')[Quelle]#

Erstellt eine glättende B-Spline, die dem Kriterium der kleinsten Quadrate (LSQ) genügt.

Das Ergebnis ist eine Linearkombination

\[S(x) = \sum_j c_j B_j(x; t)\]

der B-Spline-Basiselemente \(B_j(x; t)\), die minimiert

\[\sum_{j} \left( w_j \times (S(x_j) - y_j) \right)^2\]

Parameter:

xarray_like, shape (m,): Abzissen.
yarray_like, shape (m, …): Ordinaten.
tarray_like, shape (n + k + 1,).: Knoten. Knoten und Datenpunkte müssen die Schoenberg-Whitney-Bedingungen erfüllen.
kint, optional: B-Spline-Grad. Standard ist kubisch, k = 3.
warray_like, shape (m,), optional: Gewichte für die Spline-Anpassung. Müssen positiv sein. Wenn None, dann sind die Gewichte alle gleich. Standard ist None.
axisint, optional: Interpolationsachse. Standard ist Null.
check_finitebool, optional: Ob überprüft werden soll, ob die Eingabearrays nur endliche Zahlen enthalten. Das Deaktivieren kann die Leistung verbessern, kann aber zu Problemen führen (Abstürze, Terminierungsprobleme), wenn die Eingaben Unendlichkeitswerte oder NaNs enthalten. Standard ist True.
methodstr, optional: Methode zur Lösung des linearen LSQ-Problems. Zulässige Werte sind „norm-eq“ (Konstruiert und löst explizit das normale Gleichungssystem) und „qr“ (Verwendet die QR-Zerlegung der Designmatrix). Standard ist „qr“.

Rückgabe:

bBSpline-Objekt: Ein BSpline-Objekt vom Grad k mit Knoten t.

Siehe auch

BSpline: Basisklasse, die die B-Spline-Objekte repräsentiert
make_interp_spline: eine ähnliche Factory-Funktion für interpolierende Splines
LSQUnivariateSpline: eine FITPACK-basierte Spline-Fitting-Routine
splrep: eine FITPACK-basierte Fitting-Routine

Hinweise

Die Anzahl der Datenpunkte muss größer sein als der Spline-Grad k.

Knoten t müssen die Schoenberg-Whitney-Bedingungen erfüllen, d.h. es muss eine Teilmenge von Datenpunkten x[j] geben, so dass t[j] < x[j] < t[j+k+1] für j=0, 1,...,n-k-2.

Beispiele

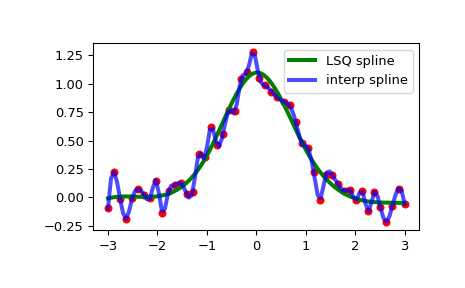
Generieren einiger verrauschter Daten

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> x = np.linspace(-3, 3, 50)
>>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(50)

Nun wird eine glättende kubische Spline mit vordefinierten inneren Knoten angepasst. Hier machen wir den Knotenvektor (k+1)-regulär, indem wir Randknoten hinzufügen

>>> from scipy.interpolate import make_lsq_spline, BSpline
>>> t = [-1, 0, 1]
>>> k = 3
>>> t = np.r_[(x[0],)*(k+1),
...           t,
...           (x[-1],)*(k+1)]
>>> spl = make_lsq_spline(x, y, t, k)

Zum Vergleich konstruieren wir auch eine interpolierende Spline für denselben Datensatz

>>> from scipy.interpolate import make_interp_spline
>>> spl_i = make_interp_spline(x, y)

Beide plotten

>>> xs = np.linspace(-3, 3, 100)
>>> plt.plot(x, y, 'ro', ms=5)
>>> plt.plot(xs, spl(xs), 'g-', lw=3, label='LSQ spline')
>>> plt.plot(xs, spl_i(xs), 'b-', lw=3, alpha=0.7, label='interp spline')
>>> plt.legend(loc='best')
>>> plt.show()

../../_images/scipy-interpolate-make_lsq_spline-1_00_00.png

NaN-Behandlung: Wenn die Eingabearrays nan-Werte enthalten, ist das Ergebnis nicht nützlich, da die zugrunde liegenden Spline-Fitting-Routinen nicht mit nan umgehen können. Eine Umgehungslösung besteht darin, Nullen als Gewichte für Not-a-Number-Datenpunkte zu verwenden

>>> y[8] = np.nan
>>> w = np.isnan(y)
>>> y[w] = 0.
>>> tck = make_lsq_spline(x, y, t, w=~w)

Beachten Sie die Notwendigkeit, ein nan durch einen numerischen Wert zu ersetzen (der genaue Wert spielt keine Rolle, solange das entsprechende Gewicht Null ist.)