scipy.ndimage.

distance_transform_bf#

scipy.ndimage.distance_transform_bf(input, metric='euclidean', sampling=None, return_distances=True, return_indices=False, distances=None, indices=None)[Quelle]#

Distanztransformationsfunktion mit einem Brute-Force-Algorithmus.

Diese Funktion berechnet die Distanztransformation des input, indem jedes Vordergrundelement (nicht-Null) durch seine kürzeste Distanz zum Hintergrund (jedes Null-wertige Element) ersetzt wird.

Zusätzlich zur Distanztransformation kann die Merkmals-Transformation berechnet werden. In diesem Fall wird der Index des nächstgelegenen Hintergrundelements zu jedem Vordergrundelement in einem separaten Array zurückgegeben.

Parameter:

inputarray_like: Eingabe
metric{‘euclidean’, ‘taxicab’, ‘chessboard’}, optional: ‘cityblock’ und ‘manhattan’ sind ebenfalls gültig und werden auf ‘taxicab’ abgebildet. Der Standardwert ist ‘euclidean’.
samplingfloat, oder Sequenz von float, optional: Dieser Parameter wird nur verwendet, wenn metric ‘euclidean’ ist. Abstand der Elemente entlang jeder Dimension. Wenn es sich um eine Sequenz handelt, muss sie die Länge des Eingangsrangs haben; wenn es sich um eine einzelne Zahl handelt, wird diese für alle Achsen verwendet. Wenn nicht angegeben, wird ein Gitterabstand von eins angenommen.
return_distancesbool, optional: Ob die Distanztransformation berechnet werden soll. Standard ist True.
return_indicesbool, optional: Ob die Merkmals-Transformation berechnet werden soll. Standard ist False.
distancesndarray, optional: Ein Ausgabearray zum Speichern der berechneten Distanztransformation anstelle der Rückgabe. return_distances muss True sein. Es muss die gleiche Form wie input haben und vom Typ float64 sein, wenn metric ‘euclidean’ ist, ansonsten uint32.
indicesint32 ndarray, optional: Ein Ausgabe-Array zum Speichern der berechneten Merkmals-Transformation anstelle ihrer Rückgabe. return_indicies muss True sein. Seine Form muss (input.ndim,) + input.shape sein.

Rückgabe:

distancesndarray, optional: Die berechnete Distanztransformation. Zurückgegeben nur, wenn return_distances True ist und distances nicht angegeben wurde. Sie hat die gleiche Form wie das Eingabearray.
indicesint32 ndarray, optional: Die berechnete Merkmals-Transformation. Sie hat ein Array in Form des Eingangs für jede Dimension des Eingangs. Siehe Dokumentation zu distance_transform_edt für ein Beispiel. Zurückgegeben nur, wenn return_indices True ist und indices nicht angegeben wurde.

Siehe auch

distance_transform_cdt: Schnellere Distanztransformation für Taxicab- und Schachbrettmetriken
distance_transform_edt: Schnellere Distanztransformation für Euklidische Metrik

Hinweise

Diese Funktion verwendet einen langsamen Brute-Force-Algorithmus. Sehen Sie auch die Funktion distance_transform_cdt für effizientere Taxicab- [1] und Schachbrettalgorithmen [2].

Referenzen

[1]

Taxicab-Distanz. Wikipedia, 2023. https://en.wikipedia.org/wiki/Taxicab_geometry

[2]

Schachbrett-Distanz. Wikipedia, 2023. https://en.wikipedia.org/wiki/Chebyshev_distance

Beispiele

Importieren Sie die notwendigen Module.

>>> import numpy as np
>>> from scipy.ndimage import distance_transform_bf
>>> import matplotlib.pyplot as plt
>>> from mpl_toolkits.axes_grid1 import ImageGrid

Zuerst erstellen wir ein kleines binäres Bild.

>>> def add_circle(center_x, center_y, radius, image, fillvalue=1):
...     # fill circular area with 1
...     xx, yy = np.mgrid[:image.shape[0], :image.shape[1]]
...     circle = (xx - center_x) ** 2 + (yy - center_y) ** 2
...     circle_shape = np.sqrt(circle) < radius
...     image[circle_shape] = fillvalue
...     return image
>>> image = np.zeros((100, 100), dtype=np.uint8)
>>> image[35:65, 20:80] = 1
>>> image = add_circle(28, 65, 10, image)
>>> image = add_circle(37, 30, 10, image)
>>> image = add_circle(70, 45, 20, image)
>>> image = add_circle(45, 80, 10, image)

Als Nächstes richten wir die Abbildung ein.

>>> fig = plt.figure(figsize=(8, 8))  # set up the figure structure
>>> grid = ImageGrid(fig, 111, nrows_ncols=(2, 2), axes_pad=(0.4, 0.3),
...                  label_mode="1", share_all=True,
...                  cbar_location="right", cbar_mode="each",
...                  cbar_size="7%", cbar_pad="2%")
>>> for ax in grid:
...     ax.axis('off')  # remove axes from images

Das obere linke Bild ist das ursprüngliche binäre Bild.

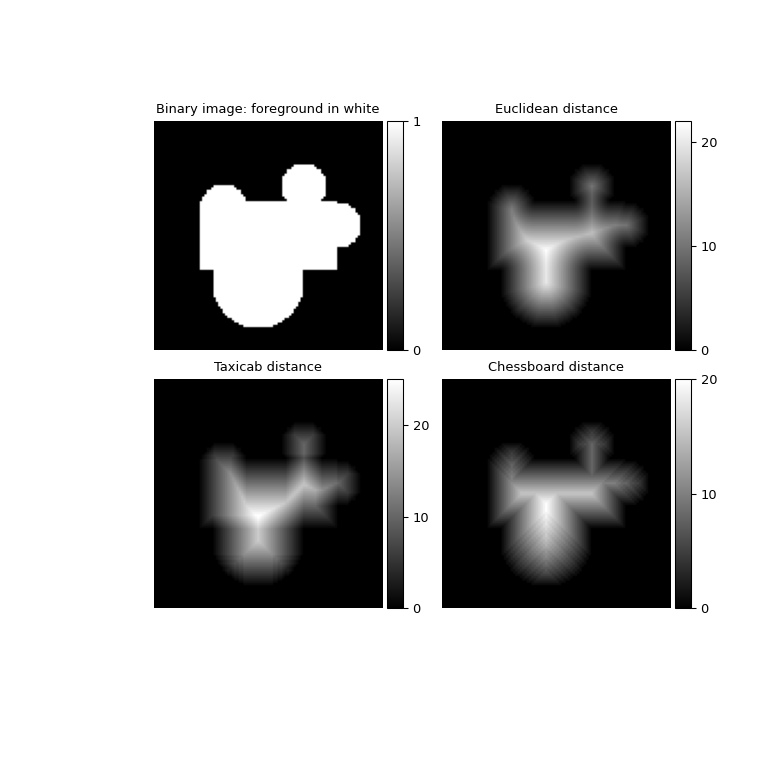
>>> binary_image = grid[0].imshow(image, cmap='gray')
>>> cbar_binary_image = grid.cbar_axes[0].colorbar(binary_image)
>>> cbar_binary_image.set_ticks([0, 1])
>>> grid[0].set_title("Binary image: foreground in white")

Die Distanztransformation berechnet die Distanz zwischen Vordergrundpixeln und dem Bildhintergrund gemäß einer Distanzmetrik. Verfügbare Metriken in distance_transform_bf sind: euclidean (Standard), taxicab und chessboard. Das obere rechte Bild enthält die Distanztransformation basierend auf der euclidean Metrik.

>>> distance_transform_euclidean = distance_transform_bf(image)
>>> euclidean_transform = grid[1].imshow(distance_transform_euclidean,
...                                      cmap='gray')
>>> cbar_euclidean = grid.cbar_axes[1].colorbar(euclidean_transform)
>>> colorbar_ticks = [0, 10, 20]
>>> cbar_euclidean.set_ticks(colorbar_ticks)
>>> grid[1].set_title("Euclidean distance")

Das untere linke Bild enthält die Distanztransformation mit der taxicab Metrik.

>>> distance_transform_taxicab = distance_transform_bf(image,
...                                                    metric='taxicab')
>>> taxicab_transformation = grid[2].imshow(distance_transform_taxicab,
...                                         cmap='gray')
>>> cbar_taxicab = grid.cbar_axes[2].colorbar(taxicab_transformation)
>>> cbar_taxicab.set_ticks(colorbar_ticks)
>>> grid[2].set_title("Taxicab distance")

Schließlich enthält das untere rechte Bild die Distanztransformation mit der chessboard Metrik.

>>> distance_transform_cb = distance_transform_bf(image,
...                                               metric='chessboard')
>>> chessboard_transformation = grid[3].imshow(distance_transform_cb,
...                                            cmap='gray')
>>> cbar_taxicab = grid.cbar_axes[3].colorbar(chessboard_transformation)
>>> cbar_taxicab.set_ticks(colorbar_ticks)
>>> grid[3].set_title("Chessboard distance")
>>> plt.show()

../../_images/scipy-ndimage-distance_transform_bf-1.png