scipy.ndimage.

distance_transform_cdt

scipy.ndimage.distance_transform_cdt(input, metric='chessboard', return_distances=True, return_indices=False, distances=None, indices=None)

Distanztransformation für Chamfer-artige Transformationen.

Diese Funktion berechnet die Distanztransformation des input, indem jedes Vordergrundelement (nicht-Null) durch seine kürzeste Distanz zum Hintergrund (jedes Null-wertige Element) ersetzt wird.

Zusätzlich zur Distanztransformation kann die Merkmals-Transformation berechnet werden. In diesem Fall wird der Index des nächstgelegenen Hintergrundelements zu jedem Vordergrundelement in einem separaten Array zurückgegeben.

Parameter:

inputarray_like

Eingabe. Werte von 0 werden als Hintergrund behandelt.

metric{‘chessboard’, ‘taxicab’} oder array_like, optional

Das metric bestimmt die Art des Chamferings. Wenn das metric gleich ‘taxicab’ ist, wird eine Struktur mithilfe von generate_binary_structure mit einer quadrierten Distanz von 1 generiert. Wenn das metric gleich ‘chessboard’ ist, wird ein metric mithilfe von generate_binary_structure mit einer quadrierten Distanz gleich der Dimensionalität des Arrays generiert. Diese Auswahl entspricht den gängigen Interpretationen der Distanzmetriken ‘taxicab’ und ‘chessboard’ in zwei Dimensionen. Ein benutzerdefiniertes Metrik kann in Form einer Matrix bereitgestellt werden, wobei jede Dimension eine Länge von drei hat. ‘cityblock’ und ‘manhattan’ sind ebenfalls gültig und werden auf ‘taxicab’ abgebildet. Der Standardwert ist ‘chessboard’.

return_distancesbool, optional

Ob die Distanztransformation berechnet werden soll. Standard ist True.

return_indicesbool, optional

Ob die Merkmals-Transformation berechnet werden soll. Standard ist False.

distancesint32 ndarray, optional

Ein Ausgabe-Array zum Speichern der berechneten Distanztransformation anstelle ihrer Rückgabe. return_distances muss True sein. Es muss die gleiche Form wie input haben.

indicesint32 ndarray, optional

Ein Ausgabe-Array zum Speichern der berechneten Merkmals-Transformation anstelle ihrer Rückgabe. return_indicies muss True sein. Seine Form muss (input.ndim,) + input.shape sein.

Rückgabe:

distancesint32 ndarray, optional

Die berechnete Distanztransformation. Wird nur zurückgegeben, wenn return_distances True ist und distances nicht angegeben wurde. Sie hat die gleiche Form wie das Eingabe-Array.

indicesint32 ndarray, optional

Die berechnete Merkmals-Transformation. Sie hat ein Array von der Form der Eingabe für jede Dimension der Eingabe. Siehe Dokumentation von distance_transform_edt für ein Beispiel. Wird nur zurückgegeben, wenn return_indices True ist und indices nicht angegeben wurde.

Siehe auch

distance_transform_edt

Schnelle Distanztransformation für die euklidische Metrik

distance_transform_bf

Distanztransformation für verschiedene Metriken mithilfe eines langsameren Brute-Force-Algorithmus

Beispiele

Probieren Sie es in Ihrem Browser aus!

Importieren Sie die notwendigen Module.

>>> import numpy as np
>>> from scipy.ndimage import distance_transform_cdt
>>> import matplotlib.pyplot as plt
>>> from mpl_toolkits.axes_grid1 import ImageGrid

Erstellen Sie zuerst ein Spiel-Binärbild.

>>> def add_circle(center_x, center_y, radius, image, fillvalue=1):
...     # fill circular area with 1
...     xx, yy = np.mgrid[:image.shape[0], :image.shape[1]]
...     circle = (xx - center_x) ** 2 + (yy - center_y) ** 2
...     circle_shape = np.sqrt(circle) < radius
...     image[circle_shape] = fillvalue
...     return image
>>> image = np.zeros((100, 100), dtype=np.uint8)
>>> image[35:65, 20:80] = 1
>>> image = add_circle(28, 65, 10, image)
>>> image = add_circle(37, 30, 10, image)
>>> image = add_circle(70, 45, 20, image)
>>> image = add_circle(45, 80, 10, image)

Richten Sie als Nächstes die Figur ein.

>>> fig = plt.figure(figsize=(5, 15))
>>> grid = ImageGrid(fig, 111, nrows_ncols=(3, 1), axes_pad=(0.5, 0.3),
...                  label_mode="1", share_all=True,
...                  cbar_location="right", cbar_mode="each",
...                  cbar_size="7%", cbar_pad="2%")
>>> for ax in grid:
...     ax.axis('off')
>>> top, middle, bottom = grid
>>> colorbar_ticks = [0, 10, 20]

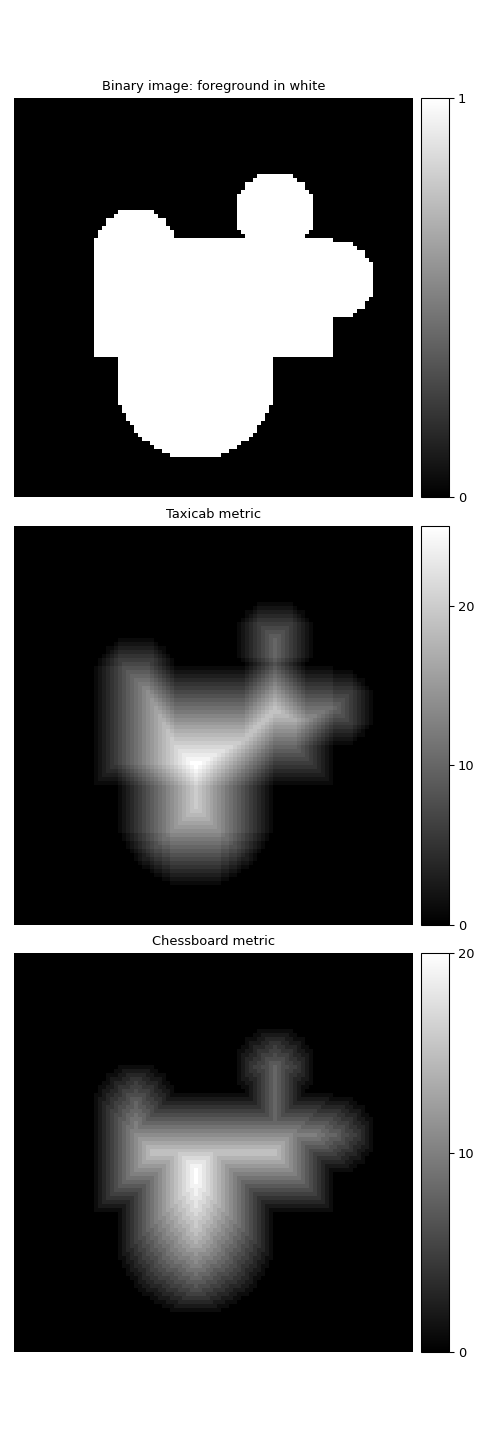
Das obere Bild enthält das ursprüngliche Binärbild.

>>> binary_image = top.imshow(image, cmap='gray')
>>> cbar_binary_image = top.cax.colorbar(binary_image)
>>> cbar_binary_image.set_ticks([0, 1])
>>> top.set_title("Binary image: foreground in white")

Das mittlere Bild enthält die Distanztransformation unter Verwendung der taxicab-Metrik.

>>> distance_taxicab = distance_transform_cdt(image, metric="taxicab")
>>> taxicab_transform = middle.imshow(distance_taxicab, cmap='gray')
>>> cbar_taxicab = middle.cax.colorbar(taxicab_transform)
>>> cbar_taxicab.set_ticks(colorbar_ticks)
>>> middle.set_title("Taxicab metric")

Das untere Bild enthält die Distanztransformation unter Verwendung der chessboard-Metrik.

>>> distance_chessboard = distance_transform_cdt(image,
...                                              metric="chessboard")
>>> chessboard_transform = bottom.imshow(distance_chessboard, cmap='gray')
>>> cbar_chessboard = bottom.cax.colorbar(chessboard_transform)
>>> cbar_chessboard.set_ticks(colorbar_ticks)
>>> bottom.set_title("Chessboard metric")
>>> plt.tight_layout()
>>> plt.show()

ZurückIn Tab öffnen