scipy.signal.ShortTimeFFT.

from_win_equals_dual#

classmethod ShortTimeFFT.from_win_equals_dual(desired_win, hop, fs, *, fft_mode='onesided', mfft=None, scale_to=None, phase_shift=0)[Quelle]#

Instanz erstellen, bei der Fenster und sein Dual bis auf einen Skalierungsfaktor gleich sind.

Eine Instanz wird erstellt, bei der Fenster und Dualfenster gleich sind und dem Parameter desired_win im Sinne der kleinsten Quadrate am nächsten liegen, d.h. abs(win-desired_win)**2 minimieren. Daher hat win die gleiche Länge wie desired_win. Anschließend wird ein Skalierungsfaktor gemäß dem Parameter scale_to angewendet.

Alle anderen Parameter haben die gleiche Bedeutung wie im Initialisierer.

Um ein gültiges Fenster berechnen zu können, muss desired_win ein gültiges duales STFT-Fenster für das gegebene hop-Intervall haben. Wenn dies nicht der Fall ist, wird ein ValueError ausgelöst.

Parameter:

desired_winnp.ndarray: Ein reell- oder komplexwertiges 1D-Array, das die Stichprobe des gewünschten Fensters enthält.
hopint: Die Schrittweite in Samples, um die das Fenster bei jedem Schritt verschoben wird.
fsfloat: Abtastfrequenz des Eingangssignals und des Fensters. Ihre Beziehung zum Abtastintervall T ist T = 1 / fs.
fft_mode‘twosided’, ‘centered’, ‘onesided’, ‘onesided2X’: Modus der zu verwendenden FFT (Standard 'onesided'). Siehe Eigenschaft fft_mode für Details.
mfft: int | None: Länge der FFT, wenn eine Null-Padding-FFT gewünscht wird. Wenn None (Standard), wird die Länge des Fensters win verwendet.
scale_to‘magnitude’ | ‘psd’ | ‘unitary’ | None: Wenn nicht None (Standard), wird die Fensterfunktion skaliert, sodass jede STFT-Spalte entweder ein 'magnitude'- oder ein Leistungsdichtespektrum ('psd') darstellt. Alternativ kann die STFT auf eine `unitary`-Abbildung skaliert werden, d.h. das Fenster wird durch np.sqrt(mfft) geteilt und das Dualfenster mit demselben Betrag multipliziert.
phase_shiftint | None: Wenn gesetzt, wird zu jeder Frequenz f eine lineare Phase phase_shift / mfft * f addiert. Der Standardwert von 0 stellt sicher, dass auf dem nullten Slice (in dem t=0 zentriert ist) keine Phasenverschiebung erfolgt. Siehe Eigenschaft phase_shift für weitere Details.

Siehe auch

closest_STFT_dual_window: Berechnet das STFT-Dualfenster eines gegebenen Fensters, das einem gewünschten Dualfenster am nächsten kommt.
ShortTimeFFT.spectrogram: Quadratische STFTs berechnen
ShortTimeFFT: Klasse, zu der diese Eigenschaft gehört.

Hinweise

Die Menge aller möglichen Fenster mit identischem Dual wird durch die Menge der linearen Beschränkungen aus Gl. (24) im Abschnitt Short-Time Fourier Transform des SciPy User Guide definiert. Dort wird auch abgeleitet, dass ShortTimeFFT.dual_win == ShortTimeFFT.m_pts * ShortTimeFFT.win gelten muss, damit eine STFT eine unitäre Abbildung ist.

Eine unitäre Abbildung erhält den Wert des Skalarprodukts, d.h.

\[\langle x, y\rangle = \sum_k x[k]\, \overline{y[k]} \stackrel{\stackrel{\text{unitär}}{\downarrow}}{=} \sum_{q,p} S_x[q,p]\, \overline{S_y[q,p]} = \langle S_x[q,p], S_y[q,p]\rangle\ ,\]

wobei \(S_{x,y}\) die STFT von \(x,y\) ist. Daher wird auch die Energie \(E_x=T\sum_k |x[k]|^2\) eines Signals erhalten. Dies wird auch im folgenden Beispiel veranschaulicht.

Der Grund für die Unterscheidung zwischen keiner Skalierung (d.h. Parameter scale_to ist None) und unitärer Skalierung (d.h. scale_to = 'unitary') liegt darin, dass die verwendete FFT-Funktion nicht unitär ist (d.h. der Standardwert 'backward' für den fft-Parameter norm verwendet wird).

Beispiele

Das folgende Beispiel zeigt, dass eine STFT tatsächlich unitär sein kann

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.signal import ShortTimeFFT, windows
...
>>> m, hop, std = 36, 8, 5
>>> desired_win = windows.gaussian(m, std, sym=True)
>>> SFT = ShortTimeFFT.from_win_equals_dual(desired_win, hop, fs=1/m,
...                                         fft_mode='twosided',
...                                         scale_to='unitary')
>>> np.allclose(SFT.dual_win, SFT.win * SFT.m_num)  # check if STFT is unitary
True
>>> x1, x2 = np.tile([-1, -1, 1, 1], 5), np.tile([1, -1, -1, 1], 5)
>>> np.sum(x1*x2) # scalar product is zero -> orthogonal signals
0
>>> np.sum(x1**2)  # scalar product of x1 with itself
20
>>> Sx11, Sx12 = SFT.spectrogram(x1), SFT.spectrogram(x1, x2)
>>> np.sum(Sx12)  # STFT scalar product is also zero
-4.163336342344337e-16+0j  # may vary
>>> np.sum(Sx11)  # == np.sum(x1**2)
19.999999999999996  # may vary
...
... # Do the plotting:
>>> fg1, (ax11, ax12) = plt.subplots(1, 2, tight_layout=True, figsize=(8, 4))
>>> s_fac = np.sqrt(SFT.mfft)
>>> _ = fg1.suptitle(f"Scaled Unitary Window of {m} Sample Gaussian with " +
...                  rf"{hop=}, $\sigma={std}$, Scale factor: {s_fac}")
>>> ax11.set(ylabel="Amplitude", xlabel="Samples", xlim=(0, m))
>>> ax12.set(xlabel="Frequency Bins", ylabel="Magnitude Spectrum",
...          xlim=(0, 15), ylim=(1e-5, 1.5))
>>> u_win_str = rf"Unitary $\times{s_fac:g}$"
>>> for x_, n_ in zip((desired_win, SFT.win*s_fac), ('Desired', u_win_str)):
...     ax11.plot(x_, '.-', alpha=0.5, label=n_)
...     X_ = np.fft.rfft(x_) / np.sum(abs(x_))
...     ax12.semilogy(abs(X_), '.-', alpha=0.5, label=n_)
>>> for ax_ in (ax11, ax12):
...     ax_.grid(True)
...     ax_.legend()
>>> plt.show()

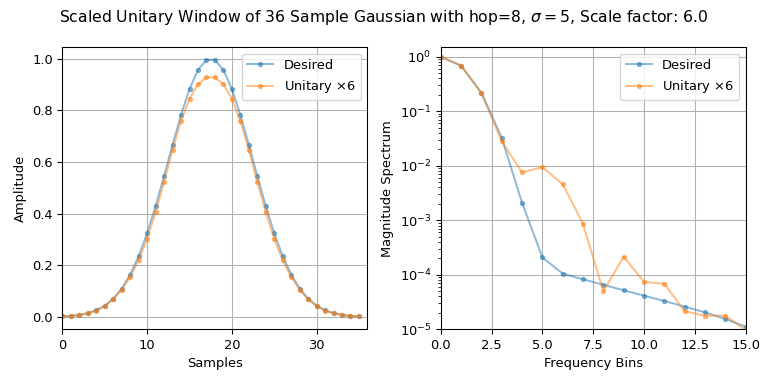
../../_images/scipy-signal-ShortTimeFFT-from_win_equals_dual-1_00_00.png

Beachten Sie, dass fftmode='twosided' verwendet wird, da wir über die gesamte Zeit-Frequenz-Ebene summieren müssen. Durch die Übergabe von scale_to='unitary' wird das Fenster SFT.win mit 1/np.sqrt(SFT.mfft) skaliert. Daher muss SFT.win im obigen Diagramm mit s_fac skaliert werden.