scipy.signal.

closest_STFT_dual_window#

scipy.signal.closest_STFT_dual_window(win, hop, desired_dual=None, *, scaled=True)[Quelle]#

Berechnet das STFT-Dualfenster eines gegebenen Fensters, das einem gewünschten Dualfenster am nächsten kommt.

Für ein gegebenes Kurzzeit-Fourier-Transformationsfenster win, das um hop Samples inkrementiert wird, wird das Dualfenster berechnet, das abs(dual_win - desired_dual)**2 minimiert, wenn scaled False ist. Wenn scaled auf True gesetzt ist, wird abs(alpha*dual_win - desired_dual)**2 minimiert, wobei alpha der optimale Skalierungsfaktor ist. Ein ValueError wird ausgelöst, wenn kein gültiges Dualfenster bestimmt werden kann.

Parameter:

winnp.ndarray: Das Fenster muss ein reell- oder komplexwertiges 1D-Array sein.
hopint: Die Schrittweite in Samples, um die das Fenster bei jedem Schritt verschoben wird.
desired_dual: np.ndarray | None: Das gewünschte Dualfenster muss ein 1D-Array mit der gleichen Länge wie win sein. Wenn auf None (Standard) gesetzt, wird angenommen, dass desired_dual das rechteckige Fenster ist, d.h. np.ones_like(win).
scaledbool: Wenn gesetzt (Standard), wird stattdessen die nächstgelegene skalierte Version des Dualfensters berechnet.

Rückgabe:

dual_winnp.ndarray: Ein Dualfenster von alpha*win (mit Hop-Intervall hop), das desired_dual am nächsten liegt. Beachten Sie, dass das Dualfenster von win dual_win/alpha ist und dass das Dualfenster von dual_win alpha*win ist. dual_win hat die gleiche Form wie win und desired_win.
alphafloat | complex: Skalierungsfaktor für win. Er ist immer eins, wenn scaled auf False gesetzt ist.

Siehe auch

ShortTimeFFT: Kurzzeit-Fourier-Transformation, die ein Dualfenster zur Berechnung der Inversen nutzen kann.
ShortTimeFFT.from_win_equals_dual: Erzeugt eine Instanz, bei der Fenster und sein Dual gleich sind.

Hinweise

Für ein gegebenes Fenster und ein hop-Intervall werden alle möglichen Dualfenster durch die hop linearen Bedingungen von Gl. (24) im Abschnitt Short-Time Fourier Transform des SciPy User Guide ausgedrückt. Daher erhöht die Verringerung von hop die Anzahl der Freiheitsgrade der Menge aller möglichen Dualfenster und verbessert die Fähigkeit, ein desired_dual besser anzunähern.

Diese Funktion kann auch verwendet werden, um Fenster zu bestimmen, die die sogenannte „Constant OverLap Add“ (COLA) Bedingung [1] erfüllen. Sie besagt, dass die Summe aller überlappenden Fensterwerte an jeder gegebenen Abtastposition die gleiche Konstante \(\alpha\) ergibt. Gl. (24) zeigt, dass dies gleichbedeutend damit ist, ein rechteckiges Dualfenster zu haben, d.h. das Dual ist alpha*np.ones(m).

Einige Beispiele für Fenster, die COLA erfüllen (entnommen aus [2])

Rechteckiges Fenster bei Überlappung von 0, 1/2, 2/3, 3/4, …
Bartlett-Fenster bei Überlappung von 1/2, 3/4, 5/6, …
Hann-Fenster bei 1/2, 2/3, 3/4, …
Jedes Fenster der Blackman-Familie bei 2/3 Überlappung
Jedes Fenster mit hop=1

Referenzen

[1]

Julius O. Smith III, „Spectral Audio Signal Processing“, Online-Buch, 2011, https://www.dsprelated.com/freebooks/sasp/

[2]

G. Heinzel, A. Ruediger und R. Schilling, „Spectrum and spectral density estimation by the Discrete Fourier transform (DFT), including a comprehensive list of window functions and some new at-top windows“, 2002, http://hdl.handle.net/11858/00-001M-0000-0013-557A-5

Beispiele

Zeigen wir, dass ein Bartlett-Fenster mit 75% Überlappung die COLA-Bedingung erfüllt

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.signal import closest_STFT_dual_window, windows
...
>>> m = 24
>>> win, w_rect = windows.bartlett(m, sym=False), np.ones(m)
>>> d_win, alpha = closest_STFT_dual_window(win, m//4, w_rect, scaled=True)
>>> print(f"COLA: {np.allclose(d_win, w_rect*alpha)}, {alpha = :g}")
COLA: True, alpha = 0.5

Wir können auch bestimmen, für welche Hop-Intervalle die COLA-Bedingung erfüllt ist

>>> hops, deviations, alphas = np.arange(1, 16, dtype=int), [], []
>>> for h_ in hops:
...     w_cola, alpha = closest_STFT_dual_window(w_rect, h_, win, scaled=True)
...     deviations.append(np.linalg.norm(w_cola - win*alpha))
...     alphas.append(alpha)
...
>>> fg0, (ax0, ax1) = plt.subplots(2, 1, sharex='all', tight_layout=True)
>>> ax0.set_title(f"COLA Window closest to a {m}-Sample Bartlett Window")
>>> ax0.set(ylabel=r"$||w_\text{cola}-\alpha w||$", xlim=(0, hops[-1]-.5))
>>> ax1.set(xlabel="Hop Interval", ylabel=r"Scaling factor $\alpha$",
...         ylim=(0, 1.25))
>>> ax0.plot(hops, deviations, 'C0.-')
>>> ax1.plot(hops, alphas, 'C1.-')
>>> for ax_ in (ax0, ax1):
...     ax_.grid()
>>> plt.show()

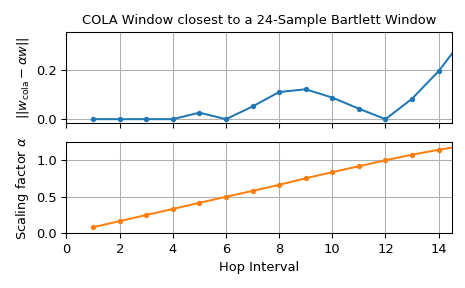
../../_images/scipy-signal-closest_STFT_dual_window-1_00_00.png

Das untere Diagramm zeigt den berechneten Skalierungsfaktor \(\alpha\) für verschiedene hops, während das obere die \(L^2\)-Norm der Differenz zwischen dem skalierten Bartlett-Fenster und dem berechneten Fenster darstellt. Da für hops von 1 bis 4 sowie für 6 und 12 die \(L^2\)-Norm der Differenz praktisch null ist, ist die COLA-Bedingung für diese erfüllt.