scipy.signal.

bessel

scipy.signal.bessel(N, Wn, btype='low', analog=False, output='ba', norm='phase', fs=None)

Bessel/Thomson digital- und Analogfilter-Design.

Entwerfen Sie einen Bessel-Filter der Ordnung N, digital oder analog, und geben Sie die Filterkoeffizienten zurück.

Parameter:

Nint

Die Ordnung des Filters.

Wnarray_like

Ein Skalar oder eine Sequenz der Länge 2, die die Grenzfrequenzen angibt (definiert durch den Parameter norm). Für analoge Filter ist Wn eine Winkelfrequenz (z.B. rad/s).

Für digitale Filter sind Wn in derselben Einheit wie fs angegeben. Standardmäßig ist fs 2 Halbzyklen/Sample, daher sind diese von 0 bis 1 normalisiert, wobei 1 die Nyquist-Frequenz ist. (Wn sind somit in Halbzyklen / Sample.)

btype{‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’}, optional

Der Filtertyp. Standard ist ‘lowpass’.

analogbool, optional

Wenn True, wird ein analoger Filter zurückgegeben, ansonsten ein digitaler Filter. (Siehe Hinweise.)

output{‘ba’, ‘zpk’, ‘sos’}, optional

Typ der Ausgabe: Zähler/Nenner ('ba'), Pol-Nullstelle ('zpk') oder Sekundärabschnitte ('sos'). Standard ist 'ba'.

norm{‘phase’, ‘delay’, ‘mag’}, optional

Normalisierung der Grenzfrequenz

phase

Der Filter wird so normalisiert, dass die Phasenantwort ihren Mittelpunkt bei der Winkelfrequenz (z.B. rad/s) Wn erreicht. Dies geschieht sowohl für Tiefpass- als auch für Hochpassfilter, daher ist dies der "phasenabgestimmte" Fall.

Die Asymptoten des Amplitudenverlaufs sind die gleichen wie bei einem Butterworth-Filter gleicher Ordnung mit einer Grenzfrequenz von Wn.

Dies ist die Standardeinstellung und entspricht der Implementierung von MATLAB.

delay

Der Filter wird so normalisiert, dass die Gruppenlaufzeit im Durchlassbereich 1/Wn (z.B. Sekunden) beträgt. Dies ist der "natürliche" Typ, der durch Lösung der Bessel-Polynome erhalten wird.

mag

Der Filter wird so normalisiert, dass die Verstärkung bei der Winkelfrequenz Wn -3 dB beträgt.

Hinzugefügt in Version 0.18.0.

fsfloat, optional

Die Abtastfrequenz des digitalen Systems.

Hinzugefügt in Version 1.2.0.

Rückgabe:

b, andarray, ndarray

Zähler- (b) und Nenner- (a) Polynome des IIR-Filters. Nur zurückgegeben, wenn output='ba'.

z, p, kndarray, ndarray, float

Nullstellen, Pole und Systemverstärkung der Übertragungsfunktion des IIR-Filters. Nur zurückgegeben, wenn output='zpk'.

sosndarray

Zweistufige Abschnittsdarstellung des IIR-Filters. Nur zurückgegeben, wenn output='sos'.

Hinweise

Auch bekannt als Thomson-Filter, hat der analoge Bessel-Filter eine maximal flache Gruppenlaufzeit und eine maximal lineare Phasenantwort mit sehr wenig Ausreißern in der Sprungantwort. [1]

Der Bessel ist von Natur aus ein analoger Filter. Diese Funktion erzeugt digitale Bessel-Filter mit der Bilinear-Transformation, die die Phasenantwort des analogen Filters nicht beibehält. Daher ist sie nur für Frequenzen unterhalb von etwa fs/4 annähernd korrekt. Um eine maximal flache Gruppenlaufzeit bei höheren Frequenzen zu erzielen, muss der analoge Bessel-Filter mit Phasen-erhaltenden Techniken transformiert werden.

Siehe besselap für Implementierungsdetails und Referenzen.

Der Parameter output='sos' wurde in 0.16.0 hinzugefügt.

Referenzen

[1]

Thomson, W.E., „Delay Networks having Maximally Flat Frequency Characteristics“, Proceedings of the Institution of Electrical Engineers, Part III, November 1949, Vol. 96, No. 44, S. 487-490.

Beispiele

Probieren Sie es in Ihrem Browser aus!

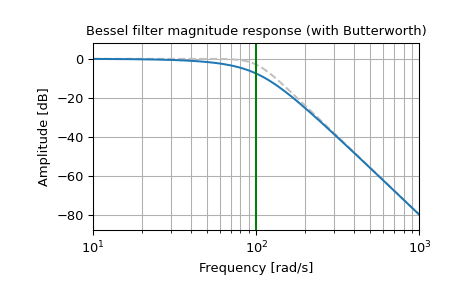
Stellen Sie die phasen-normalisierte Frequenzantwort dar, die den Zusammenhang mit der Grenzfrequenz des Butterworth-Filters (grün) zeigt

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> b, a = signal.butter(4, 100, 'low', analog=True)
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(np.abs(h)), color='silver', ls='dashed')
>>> b, a = signal.bessel(4, 100, 'low', analog=True, norm='phase')
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(np.abs(h)))
>>> plt.title('Bessel filter magnitude response (with Butterworth)')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.axvline(100, color='green')  # cutoff frequency
>>> plt.show()

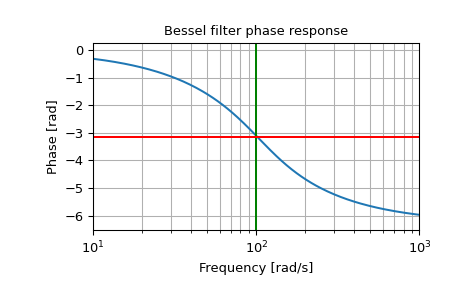
und den Phasenmittelpunkt

>>> plt.figure()
>>> plt.semilogx(w, np.unwrap(np.angle(h)))
>>> plt.axvline(100, color='green')  # cutoff frequency
>>> plt.axhline(-np.pi, color='red')  # phase midpoint
>>> plt.title('Bessel filter phase response')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Phase [rad]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.show()

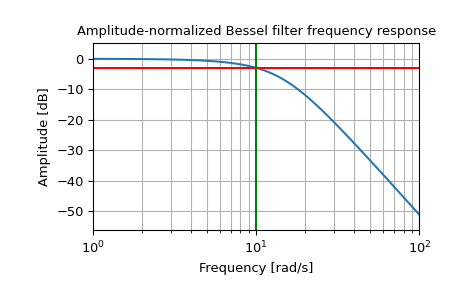
Stellen Sie die amplituden-normalisierte Frequenzantwort dar, die die -3 dB Grenzfrequenz zeigt

>>> b, a = signal.bessel(3, 10, 'low', analog=True, norm='mag')
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(np.abs(h)))
>>> plt.axhline(-3, color='red')  # -3 dB magnitude
>>> plt.axvline(10, color='green')  # cutoff frequency
>>> plt.title('Amplitude-normalized Bessel filter frequency response')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.show()

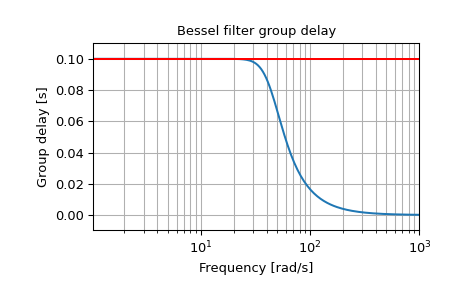
Stellen Sie den laufzeit-normalisierten Filter dar, der die maximal flache Gruppenlaufzeit von 0,1 Sekunden zeigt

>>> b, a = signal.bessel(5, 1/0.1, 'low', analog=True, norm='delay')
>>> w, h = signal.freqs(b, a)
>>> plt.figure()
>>> plt.semilogx(w[1:], -np.diff(np.unwrap(np.angle(h)))/np.diff(w))
>>> plt.axhline(0.1, color='red')  # 0.1 seconds group delay
>>> plt.title('Bessel filter group delay')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Group delay [s]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.show()

ZurückIn Tab öffnen