scipy.signal.

cheb1ord#

scipy.signal.cheb1ord(wp, ws, gpass, gstop, analog=False, fs=None)[Quelle]#

Bestimmung der Ordnung eines Chebyshev-Filters vom Typ I.

Gibt die Ordnung des niedrigsten digitalen oder analogen Chebyshev-Filters vom Typ I zurück, der im Durchlassbereich nicht mehr als gpass dB verliert und eine Dämpfung von mindestens gstop dB im Sperrbereich hat.

Parameter:

wp, wsfloat

Grenzfrequenzen des Durchlass- und Sperrbereichs.

Für digitale Filter sind diese in denselben Einheiten wie fs angegeben. Standardmäßig ist fs 2 Halbzyklen/Sample, sodass diese von 0 bis 1 normalisiert sind, wobei 1 die Nyquist-Frequenz ist. (wp und ws sind somit in Halbzyklen / Sample.) Zum Beispiel

Tiefpass: wp = 0.2, ws = 0.3

Hochpass: wp = 0.3, ws = 0.2

Bandpass: wp = [0.2, 0.5], ws = [0.1, 0.6]

Bandstopp: wp = [0.1, 0.6], ws = [0.2, 0.5]

Für analoge Filter sind wp und ws Winkelgeschwindigkeiten (z. B. rad/s).

gpassfloat

Der maximale Verlust im Durchlassbereich (dB).

gstopfloat

Die minimale Dämpfung im Sperrbereich (dB).

analogbool, optional

Wenn True, wird ein analoger Filter zurückgegeben, andernfalls ein digitaler Filter.

fsfloat, optional

Die Abtastfrequenz des digitalen Systems.

Hinzugefügt in Version 1.2.0.

Rückgabe:

ordint: Die niedrigste Ordnung für einen Chebyshev-Filter vom Typ I, der die Spezifikationen erfüllt.
wnndarray oder float: Die natürliche Frequenz des Chebyshev-Filters (die „3-dB-Frequenz“) zur Verwendung mit cheby1, um Filterergebnisse zu erzielen. Wenn fs angegeben ist, ist dies in derselben Einheit, und fs muss ebenfalls an cheby1 übergeben werden.

Siehe auch

cheby1: Filterentwurf unter Verwendung von Ordnung und kritischen Punkten
buttord: Ordnung und kritische Punkte aus Durchlass- und Sperrbereichsspezifikationen ermitteln
cheb2ord, ellipord
iirfilter: Allgemeines Filterdesign unter Verwendung von Ordnung und kritischen Frequenzen
iirdesign: Allgemeines Filterdesign mit Spezifikationen für Durchlass- und Sperrbereich

Beispiele

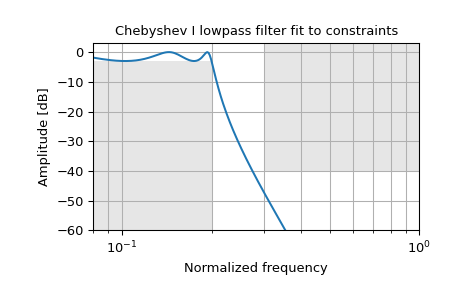
Entwerfen Sie ein digitales Tiefpassfilter, sodass der Durchlassbereich bis zu 0,2*(fs/2) innerhalb von 3 dB liegt, während oberhalb von 0,3*(fs/2) eine Unterdrückung von mindestens -40 dB erreicht wird. Plottieren Sie dessen Frequenzgang und zeigen Sie die Durchlass- und Sperrbereichsbeschränkungen in Grau an.

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> N, Wn = signal.cheb1ord(0.2, 0.3, 3, 40)
>>> b, a = signal.cheby1(N, 3, Wn, 'low')
>>> w, h = signal.freqz(b, a)
>>> plt.semilogx(w / np.pi, 20 * np.log10(abs(h)))
>>> plt.title('Chebyshev I lowpass filter fit to constraints')
>>> plt.xlabel('Normalized frequency')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.grid(which='both', axis='both')
>>> plt.fill([.01, 0.2, 0.2, .01], [-3, -3, -99, -99], '0.9', lw=0) # stop
>>> plt.fill([0.3, 0.3,   2,   2], [ 9, -40, -40,  9], '0.9', lw=0) # pass
>>> plt.axis([0.08, 1, -60, 3])
>>> plt.show()

../../_images/scipy-signal-cheb1ord-1.png