scipy.signal.

iirdesign#

scipy.signal.iirdesign(wp, ws, gpass, gstop, analog=False, ftype='ellip', output='ba', fs=None)[Quelle]#

Vollständiges Design von digitalen und analogen IIR-Filtern.

Konstruiert basierend auf Durchlass- und Sperrbereichsfrequenzen sowie Verstärkungen einen analogen oder digitalen IIR-Filter minimaler Ordnung für einen gegebenen Basistyp. Gibt die Ausgabe in Form von Zähler, Nenner ('ba'), Pol-Nullstelle ('zpk') oder zweistufigen Abschnitten ('sos') zurück.

Parameter:

wp, wsfloat oder Array-ähnlich, Form (2,)

Grenzfrequenzen des Durchlass- und Sperrbereichs. Mögliche Werte sind Skalare (für Tiefpass- und Hochpassfilter) oder Bereiche (für Bandpass- und Bandstoppfilter). Für digitale Filter sind dies dieselben Einheiten wie fs. Standardmäßig ist fs 2 Halbzylüsse/Sample, daher sind diese von 0 bis 1 normalisiert, wobei 1 die Nyquist-Frequenz ist. Zum Beispiel:

Tiefpass: wp = 0.2, ws = 0.3

Hochpass: wp = 0.3, ws = 0.2

Bandpass: wp = [0.2, 0.5], ws = [0.1, 0.6]

Bandstopp: wp = [0.1, 0.6], ws = [0.2, 0.5]

Für analoge Filter sind wp und ws Winkelgeschwindigkeiten (z. B. rad/s). Beachten Sie, dass für Bandpass- und Bandstoppfilter der Durchlassbereich strikt innerhalb des Sperrbereichs liegen muss oder umgekehrt. Beachten Sie auch, dass die Grenzfrequenz an den Bandkanten für IIR-Filter als Halbleistung, also -3dB, und nicht als Halbamplitude (-6dB) wie bei scipy.signal.fiwin definiert ist.

gpassfloat

Der maximale Verlust im Durchlassbereich (dB).

gstopfloat

Die minimale Dämpfung im Sperrbereich (dB).

analogbool, optional

Wenn True, wird ein analoger Filter zurückgegeben, andernfalls ein digitaler Filter.

ftypestr, optional

Der Typ des zu entwerfenden IIR-Filters

Butterworth : ‘butter’

Tschebyscheff I : ‘cheby1’

Tschebyscheff II : ‘cheby2’

Cauer/Elliptisch: ‘ellip’

output{‘ba’, ‘zpk’, ‘sos’}, optional

Filterform der Ausgabe

zweistufige Abschnitte (empfohlen): ‘sos’

Zähler/Nenner (Standard): ‘ba’

Pol-Nullstelle: ‘zpk’

Im Allgemeinen wird die Form der zweistufigen Abschnitte ('sos') empfohlen, da die Ableitung der Koeffizienten für die Zähler/Nenner-Form ('ba') mit numerischen Instabilitäten behaftet ist. Aus Gründen der Abwärtskompatibilität ist die Standardform die Zähler/Nenner-Form ('ba'), wobei sich 'b' und 'a' in 'ba' auf die gängigen Namen der verwendeten Koeffizienten beziehen.

Hinweis: Die Verwendung der Form der zweistufigen Abschnitte ('sos') ist manchmal mit zusätzlichen Rechenkosten verbunden: für datenintensive Anwendungsfälle wird daher auch die Untersuchung der Zähler/Nenner-Form ('ba') empfohlen.

fsfloat, optional

Die Abtastfrequenz des digitalen Systems.

Hinzugefügt in Version 1.2.0.

Rückgabe:

b, andarray, ndarray: Zähler- (b) und Nenner- (a) Polynome des IIR-Filters. Nur zurückgegeben, wenn output='ba'.
z, p, kndarray, ndarray, float: Nullstellen, Pole und Systemverstärkung der Übertragungsfunktion des IIR-Filters. Nur zurückgegeben, wenn output='zpk'.
sosndarray: Zweistufige Abschnittsdarstellung des IIR-Filters. Nur zurückgegeben, wenn output='sos'.

Siehe auch

butter: Filterentwurf unter Verwendung von Ordnung und kritischen Punkten
cheby1, cheby2, ellip, bessel
buttord: Ordnung und kritische Punkte aus Durchlass- und Sperrbereichsspezifikationen ermitteln
cheb1ord, cheb2ord, ellipord
iirfilter: Allgemeines Filterdesign unter Verwendung von Ordnung und kritischen Frequenzen

Hinweise

Der Parameter output='sos' wurde in 0.16.0 hinzugefügt.

Beispiele

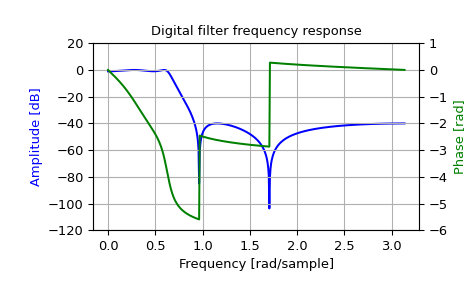
>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import matplotlib.ticker

>>> wp = 0.2
>>> ws = 0.3
>>> gpass = 1
>>> gstop = 40

>>> system = signal.iirdesign(wp, ws, gpass, gstop)
>>> w, h = signal.freqz(*system)

>>> fig, ax1 = plt.subplots()
>>> ax1.set_title('Digital filter frequency response')
>>> ax1.plot(w, 20 * np.log10(abs(h)), 'b')
>>> ax1.set_ylabel('Amplitude [dB]', color='b')
>>> ax1.set_xlabel('Frequency [rad/sample]')
>>> ax1.grid(True)
>>> ax1.set_ylim([-120, 20])
>>> ax2 = ax1.twinx()
>>> phase = np.unwrap(np.angle(h))
>>> ax2.plot(w, phase, 'g')
>>> ax2.set_ylabel('Phase [rad]', color='g')
>>> ax2.grid(True)
>>> ax2.axis('tight')
>>> ax2.set_ylim([-6, 1])
>>> nticks = 8
>>> ax1.yaxis.set_major_locator(matplotlib.ticker.LinearLocator(nticks))
>>> ax2.yaxis.set_major_locator(matplotlib.ticker.LinearLocator(nticks))

../../_images/scipy-signal-iirdesign-1.png