scipy.signal.

cspline1d_eval#

scipy.signal.cspline1d_eval(cj, newx, dx=1.0, x0=0)[Quelle]#

Evaluiert einen kubischen Spline an einem neuen Satz von Punkten.

dx ist der alte Abtastabstand, während x0 der alte Ursprung war. Anders ausgedrückt, die alten Abtastpunkte (Knotenpunkte) für die cj Kubische Spline-Koeffizienten darstellen, lagen bei gleichmäßigen Punkten von

oldx = x0 + j*dx j=0…N-1, mit N=len(cj)

Ränder werden mit spiegelbildlichen Randbedingungen behandelt.

Parameter:

cjndarray: Kubische Spline-Koeffizienten
newxndarray: Neuer Satz von Punkten.
dxfloat, optional: Alter Abtastabstand, der Standardwert ist 1.0.
x0int, optional: Alter Ursprung, der Standardwert ist 0.

Rückgabe:

resndarray: Ausgewertete kubische Spline-Punkte.

Siehe auch

cspline1d: Berechnet kubische Spline-Koeffizienten für ein Rang-1-Array.

Beispiele

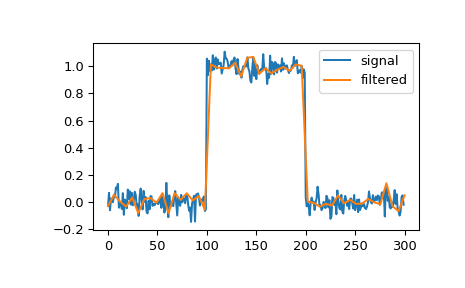
Wir können ein Signal filtern, um hochfrequentes Rauschen mit einem kubischen Spline zu reduzieren und zu glätten.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import cspline1d, cspline1d_eval
>>> rng = np.random.default_rng()
>>> sig = np.repeat([0., 1., 0.], 100)
>>> sig += rng.standard_normal(len(sig))*0.05  # add noise
>>> time = np.linspace(0, len(sig))
>>> filtered = cspline1d_eval(cspline1d(sig), time)
>>> plt.plot(sig, label="signal")
>>> plt.plot(time, filtered, label="filtered")
>>> plt.legend()
>>> plt.show()

../../_images/scipy-signal-cspline1d_eval-1.png