scipy.signal.

dimpulse

scipy.signal.dimpulse(system, x0=None, t=None, n=None)

Impulsantwort eines diskreten Zeitsystems.

Parameter:

systemdlti | tuple

Eine Instanz der LTI-Klasse dlti oder ein Tupel, das das System beschreibt. Die Anzahl der Elemente im Tupel bestimmt die Interpretation. D. h.

• system: Instanz der Klasse LTI dlti. Beachten Sie, dass abgeleitete Instanzen, wie z. B. Instanzen von TransferFunction, ZerosPolesGain oder StateSpace, ebenfalls zulässig sind.

• (num, den, dt): Rationale Polynome, wie in TransferFunction beschrieben. Die Koeffizienten der Polynome sollten in absteigender Exponentenreihenfolge angegeben werden, z.B. z² + 3z + 5 würde als [1, 3, 5] dargestellt werden.

• (zeros, poles, gain, dt): Nullstellen-, Pol-, Verstärkungsform, wie in ZerosPolesGain beschrieben.

• (A, B, C, D, dt): Zustandsraumform, wie in StateSpace beschrieben.

x0array_like, optional

Anfangszustandsvektor. Standardmäßig Null.

tarray_like, optional

Zeitpunkte. Wird berechnet, wenn nicht gegeben.

nint, optional

Die Anzahl der zu berechnenden Zeitpunkte (wenn t nicht angegeben ist).

Rückgabe:

toutndarray

Zeitwerte für die Ausgabe als 1D-Array.

youtTupel von ndarray

Impulsantwort des Systems. Jedes Element des Tupels repräsentiert die Ausgabe des Systems basierend auf einem Impuls in jedem Eingang.

Siehe auch

impulse, dstep, dlsim, cont2discrete

Beispiele

Probieren Sie es in Ihrem Browser aus!

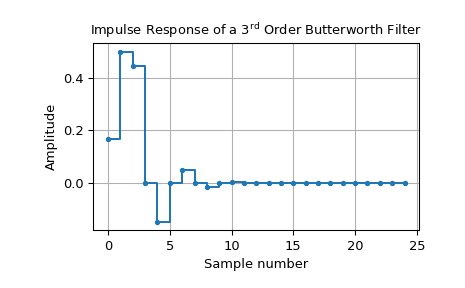
>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
...
>>> dt = 1  # sampling interval is one => time unit is sample number
>>> bb, aa = signal.butter(3, 0.25, fs=1/dt)
>>> t, y = signal.dimpulse((bb, aa, dt), n=25)
...
>>> fig0, ax0 = plt.subplots()
>>> ax0.step(t, np.squeeze(y), '.-', where='post')
>>> ax0.set_title(r"Impulse Response of a $3^\text{rd}$ Order Butterworth Filter")
>>> ax0.set(xlabel='Sample number', ylabel='Amplitude')
>>> ax0.grid()
>>> plt.show()

ZurückIn Tab öffnen