scipy.signal.

dstep#

scipy.signal.dstep(system, x0=None, t=None, n=None)[Quellcode]#

Sprungantwort eines diskreten Systems.

Parameter:

systemdlti | tuple

Eine Instanz der LTI-Klasse dlti oder ein Tupel, das das System beschreibt. Die Anzahl der Elemente im Tupel bestimmt die Interpretation. D. h.

system: Instanz der LTI-Klasse dlti. Beachten Sie, dass abgeleitete Instanzen, wie z.B. Instanzen von TransferFunction, ZerosPolesGain oder StateSpace, ebenfalls erlaubt sind.
(num, den, dt): Rationale Polynome, wie in TransferFunction beschrieben. Die Koeffizienten der Polynome sollten in absteigender Exponentenreihenfolge angegeben werden, z.B. z² + 3z + 5 würde als [1, 3, 5] dargestellt werden.
(zeros, poles, gain, dt): Nullstellen-, Pol-, Verstärkungsform, wie in ZerosPolesGain beschrieben.
(A, B, C, D, dt): Zustandsraumform, wie in StateSpace beschrieben.

x0array_like, optional

Anfangszustandsvektor. Standardmäßig Null.

tarray_like, optional

Zeitpunkte. Wird berechnet, wenn nicht gegeben.

nint, optional

Die Anzahl der zu berechnenden Zeitpunkte (wenn t nicht angegeben ist).

Rückgabe:

toutndarray: Ausgabezeitpunkte als 1D-Array.
youtTupel von ndarray: Sprungantwort des Systems. Jedes Element des Tupels repräsentiert die Ausgabe des Systems basierend auf einer Sprungantwort auf jeden Eingang.

Siehe auch

step, dimpulse, dlsim, cont2discrete

Beispiele

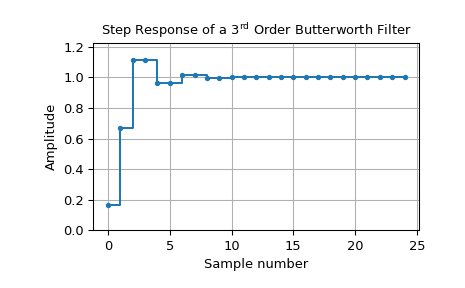
Das folgende Beispiel zeigt, wie ein digitaler Butterworth-Filter erstellt und seine Sprungantwort geplottet werden kann

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
...
>>> dt = 1  # sampling interval is one => time unit is sample number
>>> bb, aa = signal.butter(3, 0.25, fs=1/dt)
>>> t, y = signal.dstep((bb, aa, dt), n=25)
...
>>> fig0, ax0 = plt.subplots()
>>> ax0.step(t, np.squeeze(y), '.-', where='post')
>>> ax0.set_title(r"Step Response of a $3^\text{rd}$ Order Butterworth Filter")
>>> ax0.set(xlabel='Sample number', ylabel='Amplitude', ylim=(0, 1.1*np.max(y)))
>>> ax0.grid()
>>> plt.show()