scipy.signal.

envelope#

scipy.signal.envelope(z, bp_in=(1, None), *, n_out=None, squared=False, residual='lowpass', axis=-1)[Quelle]#

Berechnet die Einhüllende eines reellen oder komplexwertigen Signals.

Parameter:

zndarray: Reelles oder komplexwertiges Eingangssignal, das aus n Samples und mit einem Abtastintervall T aufgebaut ist. z kann auch ein mehrdimensionales Array sein, wobei die Zeitachse durch axis definiert ist.
bp_intuple[int | None, int | None], optional: 2er-Tupel, das das Frequenzband bp_in[0]:bp_in[1] des Eingangsfilters definiert. Die Eckfrequenzen sind als ganzzahlige Vielfache von 1/(n*T) angegeben, wobei -n//2 <= bp_in[0] < bp_in[1] <= (n+1)//2 der zulässige Frequenzbereich ist. None-Einträge werden durch -n//2 bzw. (n+1)//2 ersetzt. Der Standardwert (1, None) entfernt den Mittelwert sowie die negativen Frequenzkomponenten.
n_outint | None, optional: Wenn nicht None, wird die Ausgabe auf n_out Samples neu abgetastet. Der Standardwert None setzt die Ausgabe auf die gleiche Länge wie die Eingabe z.
squaredbool, optional: Wenn gesetzt, wird das Quadrat der Einhüllenden zurückgegeben. Die Bandbreite der quadrierten Einhüllenden ist aufgrund der nichtlinearen Natur der verwendeten Absolutwertfunktion oft kleiner als die Bandbreite der nicht-quadrierten Einhüllenden. D.h. die eingebettete Quadratwurzelfunktion erzeugt typischerweise zusätzliche Harmonische. Der Standardwert ist False.
residualLiteral[‘lowpass’, ‘all’, None], optional: Diese Option bestimmt, welche Art von Residuum, d.h. der Signalteil, den der Eingangs-Bandpassfilter entfernt, zurückgegeben wird. 'all' gibt alles außer den Inhalten des Frequenzbandes bp_in[0]:bp_in[1] zurück, 'lowpass' gibt die Inhalte des Frequenzbandes < bp_in[0] zurück. Wenn None, wird nur die Einhüllende zurückgegeben. Standard: 'lowpass'.
axisint, optional: Achse von z, über die die Einhüllende berechnet wird. Standard ist die letzte Achse.

Rückgabe:

ndarray: Wenn der Parameter residual None ist, wird ein Array z_env mit der gleichen Form wie die Eingabe z zurückgegeben, das seine Einhüllende enthält. Andernfalls wird ein Array mit der Form (2, *z.shape) zurückgegeben, das die Arrays z_env und z_res enthält, gestapelt entlang der ersten Achse. Dies ermöglicht das Entpacken, d.h. z_env, z_res = envelope(z, residual='all'). Das Residuum z_res enthält den Signalteil, den der Eingangs-Bandpassfilter entfernt hat, abhängig vom Parameter residual. Beachten Sie, dass für reelle Signale ein reelles Residuum zurückgegeben wird. Daher werden die negativen Frequenzkomponenten von bp_in ignoriert.

Siehe auch

hilbert: Berechnet das analytische Signal mittels Hilbert-Transformation.

Hinweise

Jedes komplexwertige Signal \(z(t)\) kann durch eine reellwertige instantane Amplitude \(a(t)\) und eine reellwertige instantane Phase \(\phi(t)\) beschrieben werden, d.h. \(z(t) = a(t) \exp\!\big(j \phi(t)\big)\). Die Einhüllende ist definiert als der Absolutwert der Amplitude \(|a(t)| = |z(t)|\), was gleichzeitig der Absolutwert des Signals ist. Daher „umhüllt“ \(|a(t)|\) die Klasse aller Signale mit Amplitude \(a(t)\) und beliebiger Phase \(\phi(t)\). Für reellwertige Signale ist \(x(t) = a(t) \cos\!\big(\phi(t)\big)\) die analoge Formulierung. Daher kann \(|a(t)|\) bestimmt werden, indem \(x(t)\) mittels einer Hilbert-Transformation in ein analytisches Signal \(z_a(t)\) umgewandelt wird, d.h. \(z_a(t) = a(t) \cos\!\big(\phi(t)\big) + j a(t) \sin\!\big(\phi(t) \big)\), was ein komplexwertiges Signal mit der gleichen Einhüllenden \(|a(t)|\) erzeugt.

Die Implementierung basiert auf der Berechnung der FFT des Eingangssignals und anschließender Durchführung der erforderlichen Operationen im Fourier-Raum. Daher müssen die üblichen FFT-Vorbehalte berücksichtigt werden.

Das Signal wird als periodisch angenommen. Diskontinuitäten zwischen Signalstart und -ende können aufgrund des Gibbs-Phänomens zu unerwünschten Ergebnissen führen.
Die FFT ist langsam, wenn die Signallänge prim oder sehr lang ist. Außerdem sind die Speicheranforderungen typischerweise höher als bei einer vergleichbaren FIR/IIR-Filterimplementierung.
Der Frequenzabstand 1 / (n*T) für die Eckfrequenzen des Bandpassfilters entspricht den Frequenzen, die von scipy.fft.fftfreq(len(z), T) erzeugt werden.

Wenn die Einhüllende eines komplexwertigen Signals z ohne Bandpassfilterung gewünscht ist, d.h. bp_in=(None, None), dann entspricht die Einhüllende dem Absolutwert. Daher ist es effizienter, np.abs(z) anstelle dieser Funktion zu verwenden.

Obwohl die Berechnung der Einhüllenden basierend auf dem analytischen Signal [1] die natürliche Methode für reellwertige Signale ist, werden auch andere Methoden häufig verwendet. Die beliebteste Alternative ist wahrscheinlich der sogenannte „Quadratgesetz“-Einhüllendendetektor und seine Verwandten [2]. Diese berechnen nicht immer das korrekte Ergebnis für alle Arten von Signalen, sind aber normalerweise korrekt und typischerweise rechnerisch effizienter für die meisten Arten von Schmalbandsignalen. Die hier dargestellte Definition für eine Einhüllende ist üblich, wenn die instantane Amplitude und Phase von Interesse sind (z. B. wie in [3] beschrieben). Es gibt auch andere Konzepte, die auf der allgemeinen mathematischen Idee einer Einhüllenden beruhen [4]: Ein pragmatischer Ansatz ist, alle oberen und unteren Signalspitzen zu bestimmen und eine Spline-Interpolation zu verwenden, um die Kurven zu ermitteln [5].

Referenzen

[1]

„Analytic Signal“, Wikipedia, https://en.wikipedia.org/wiki/Analytic_signal

[2]

Lyons, Richard, „Digital envelope detection: The good, the bad, and the ugly“, IEEE Signal Processing Magazine 34.4 (2017): 183-187. PDF

[3]

T.G. Kincaid, „The complex representation of signals.“, TIS R67# MH5, General Electric Co. (1966). PDF

[4]

„Envelope (mathematics)“, Wikipedia, https://en.wikipedia.org/wiki/Envelope_(mathematics)

[5]

Yang, Yanli. „A signal theoretic approach for envelope analysis of real-valued signals.“ IEEE Access 5 (2017): 5623-5630. PDF

Beispiele

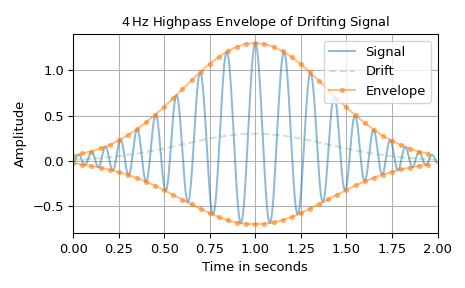
Die folgende Abbildung veranschaulicht die Einhüllende eines Signals mit variabler Frequenz und niederfrequenter Drift. Um die Drift von der Einhüllenden zu trennen, wird ein 4-Hz-Hochpassfilter verwendet. Das Niederfrequenz-Residuum des Eingangs-Bandpassfilters wird verwendet, um eine asymmetrische obere und untere Grenze zur Umhüllung des Signals zu bestimmen. Aufgrund der Glattheit der resultierenden Einhüllenden wird sie von 500 auf 40 Samples herunterabgetastet. Beachten Sie, dass die instantane Amplitude a_x und die berechnete Einhüllende x_env nicht perfekt identisch sind. Dies liegt daran, dass das Signal nicht perfekt periodisch ist und eine spektrale Überlappung von x_carrier und x_drift besteht. Daher können sie nicht vollständig durch einen Bandpassfilter getrennt werden.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.signal.windows import gaussian
>>> from scipy.signal import envelope
...
>>> n, n_out = 500, 40  # number of signal samples and envelope samples
>>> T = 2 / n  # sampling interval for 2 s duration
>>> t = np.arange(n) * T  # time stamps
>>> a_x = gaussian(len(t), 0.4/T)  # instantaneous amplitude
>>> phi_x = 30*np.pi*t + 35*np.cos(2*np.pi*0.25*t)  # instantaneous phase
>>> x_carrier = a_x * np.cos(phi_x)
>>> x_drift = 0.3 * gaussian(len(t), 0.4/T)  # drift
>>> x = x_carrier + x_drift
...
>>> bp_in = (int(4 * (n*T)), None)  # 4 Hz highpass input filter
>>> x_env, x_res = envelope(x, bp_in, n_out=n_out)
>>> t_out = np.arange(n_out) * (n / n_out) * T
...
>>> fg0, ax0 = plt.subplots(1, 1, tight_layout=True)
>>> ax0.set_title(r"$4\,$Hz Highpass Envelope of Drifting Signal")
>>> ax0.set(xlabel="Time in seconds", xlim=(0, n*T), ylabel="Amplitude")
>>> ax0.plot(t, x, 'C0-', alpha=0.5, label="Signal")
>>> ax0.plot(t, x_drift, 'C2--', alpha=0.25, label="Drift")
>>> ax0.plot(t_out, x_res+x_env, 'C1.-', alpha=0.5, label="Envelope")
>>> ax0.plot(t_out, x_res-x_env, 'C1.-', alpha=0.5, label=None)
>>> ax0.grid(True)
>>> ax0.legend()
>>> plt.show()

../../_images/scipy-signal-envelope-1_00_00.png

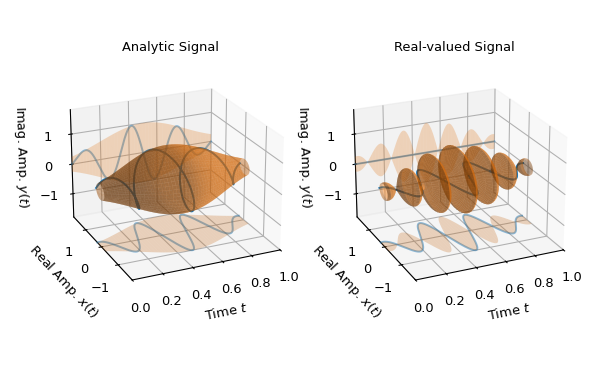
Das zweite Beispiel liefert eine geometrische Einhüllendeninterpretation komplexwertiger Signale: Die folgenden beiden Abbildungen zeigen das komplexwertige Signal als blaue 3D-Trajektorie und die Einhüllende als orangefarbene runde Röhre mit variierendem Durchmesser, d.h. als \(|a(t)| \exp(j\rho(t))\), mit \(\rho(t)\in[-\pi,\pi]\). Ebenso ist die Projektion in die 2D-reellen und imaginären Koordinatenebenen der Trajektorie und der Röhre dargestellt. Jeder Punkt des komplexwertigen Signals berührt die Oberfläche der Röhre.

Die linke Abbildung zeigt ein analytisches Signal, d.h. die Phasendifferenz zwischen Imaginär- und Realteil beträgt stets 90 Grad, was zu einer spiralförmigen Trajektorie führt. Man kann sehen, dass in diesem Fall der Realteil auch die erwartete Einhüllende hat, d.h. den Absolutwert der instantanen Amplitude darstellt.

Die rechte Abbildung zeigt den Realteil dieses analytischen Signals, interpretiert als komplexwertiges Signal, d.h. mit einem Imaginärteil von Null. Dort ist die resultierende Einhüllende nicht so glatt wie im analytischen Fall, und die instantane Amplitude in der reellen Ebene wird nicht wiederhergestellt. Wenn z_re als reelles Signal übergeben worden wäre, d.h. als z_re = z.real anstatt als z_re = z.real + 0j, wäre das Ergebnis identisch mit der linken Abbildung gewesen. Der Grund dafür ist, dass reelle Signale als der Realteil eines komplexwertigen analytischen Signals interpretiert werden.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.signal.windows import gaussian
>>> from scipy.signal import envelope
...
>>> n, T = 1000, 1/1000  # number of samples and sampling interval
>>> t = np.arange(n) * T  # time stamps for 1 s duration
>>> f_c = 3  # Carrier frequency for signal
>>> z = gaussian(len(t), 0.3/T) * np.exp(2j*np.pi*f_c*t)  # analytic signal
>>> z_re = z.real + 0j  # complex signal with zero imaginary part
...
>>> e_a, e_r = (envelope(z_, (None, None), residual=None) for z_ in (z, z_re))
...
>>> # Generate grids to visualize envelopes as 2d and 3d surfaces:
>>> E2d_t, E2_amp = np.meshgrid(t, [-1, 1])
>>> E2d_1 = np.ones_like(E2_amp)
>>> E3d_t, E3d_phi = np.meshgrid(t, np.linspace(-np.pi, np.pi, 300))
>>> ma = 1.8  # maximum axis values in real and imaginary direction
...
>>> fg0 = plt.figure(figsize=(6.2, 4.))
>>> ax00 = fg0.add_subplot(1, 2, 1, projection='3d')
>>> ax01 = fg0.add_subplot(1, 2, 2, projection='3d', sharex=ax00,
...                        sharey=ax00, sharez=ax00)
>>> ax00.set_title("Analytic Signal")
>>> ax00.set(xlim=(0, 1), ylim=(-ma, ma), zlim=(-ma, ma))
>>> ax01.set_title("Real-valued Signal")
>>> for z_, e_, ax_ in zip((z, z.real), (e_a, e_r), (ax00, ax01)):
...     ax_.set(xlabel="Time $t$", ylabel="Real Amp. $x(t)$",
...             zlabel="Imag. Amp. $y(t)$")
...     ax_.plot(t, z_.real, 'C0-', zs=-ma, zdir='z', alpha=0.5, label="Real")
...     ax_.plot_surface(E2d_t, e_*E2_amp, -ma*E2d_1, color='C1', alpha=0.25)
...     ax_.plot(t, z_.imag, 'C0-', zs=+ma, zdir='y', alpha=0.5, label="Imag.")
...     ax_.plot_surface(E2d_t, ma*E2d_1, e_*E2_amp, color='C1', alpha=0.25)
...     ax_.plot(t, z_.real, z_.imag, 'C0-', label="Signal")
...     ax_.plot_surface(E3d_t, e_*np.cos(E3d_phi), e_*np.sin(E3d_phi),
...                      color='C1', alpha=0.5, shade=True, label="Envelope")
...     ax_.view_init(elev=22.7, azim=-114.3)
>>> fg0.subplots_adjust(left=0.08, right=0.97, wspace=0.15)
>>> plt.show()

../../_images/scipy-signal-envelope-1_01_00.png