scipy.signal.

hilbert#

scipy.signal.hilbert(x, N=None, axis=-1)[Quelle]#

FFT-basierte Berechnung des analytischen Signals.

Das analytische Signal wird berechnet, indem die negativen Frequenzen herausgefiltert und die Amplituden der positiven Frequenzen im FFT-Bereich verdoppelt werden. Der Imaginärteil des Ergebnisses ist die Hilbert-Transformation des reellwertigen Eingangssignals.

Die Transformation erfolgt standardmäßig entlang der letzten Achse.

Parameter:

xarray_like: Signal-Daten. Müssen reell sein.
Nint, optional: Anzahl der Fourier-Komponenten. Standard: x.shape[axis]
axisint, optional: Achse, entlang der die Transformation durchgeführt werden soll. Standard: -1.

Rückgabe:

xandarray: Analytisches Signal von x, von jedem 1D-Array entlang axis

Siehe auch

Hüllkurve: Berechnet die Hüllkurve eines reell- oder komplexwertigen Signals.

Hinweise

Das analytische Signal x_a(t) eines reellwertigen Signals x(t) kann ausgedrückt werden als [1]

\[x_a = F^{-1}(F(x) 2U) = x + i y\ ,\]

wobei F die Fourier-Transformation ist, U die Einheitsstufenfunktion und y die Hilbert-Transformation von x ist. [2]

Mit anderen Worten, die negative Hälfte des Frequenzspektrums wird auf Null gesetzt, wodurch das reellwertige Signal in ein komplexwertiges Signal umgewandelt wird. Das Hilbert-transformierte Signal kann aus np.imag(hilbert(x)) und das ursprüngliche Signal aus np.real(hilbert(x)) erhalten werden.

Referenzen

[1]

Wikipedia, „Analytic signal“. https://en.wikipedia.org/wiki/Analytic_signal

[2]

Wikipedia, „Hilbert Transform“. https://en.wikipedia.org/wiki/Hilbert_transform

[3]

Leon Cohen, „Time-Frequency Analysis“, 1995. Kapitel 2.

[4]

Alan V. Oppenheim, Ronald W. Schafer. Discrete-Time Signal Processing, Third Edition, 2009. Kapitel 12. ISBN 13: 978-1292-02572-8

Beispiele

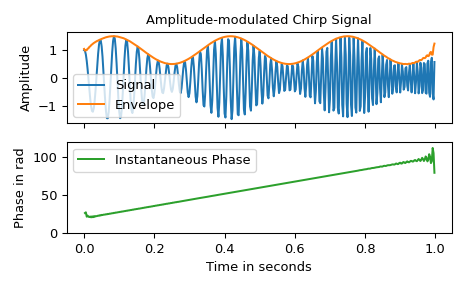
In diesem Beispiel verwenden wir die Hilbert-Transformation, um die Amplituden-Hüllkurve und die momentane Frequenz eines Amplituden-modulierten Signals zu bestimmen.

Erstellen wir einen Chirp, dessen Frequenz von 20 Hz auf 100 Hz ansteigt und wenden wir eine Amplitudenmodulation an.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import hilbert, chirp
...
>>> duration, fs = 1, 400  # 1 s signal with sampling frequency of 400 Hz
>>> t = np.arange(int(fs*duration)) / fs  # timestamps of samples
>>> signal = chirp(t, 20.0, t[-1], 100.0)
>>> signal *= (1.0 + 0.5 * np.sin(2.0*np.pi*3.0*t) )

Die Amplituden-Hüllkurve wird durch den Betrag des analytischen Signals gegeben. Die momentane Frequenz kann durch Differenzierung der momentanen Phase in Bezug auf die Zeit erhalten werden. Die momentane Phase entspricht dem Phasenwinkel des analytischen Signals.

>>> analytic_signal = hilbert(signal)
>>> amplitude_envelope = np.abs(analytic_signal)
>>> instantaneous_phase = np.unwrap(np.angle(analytic_signal))
>>> instantaneous_frequency = np.diff(instantaneous_phase) / (2.0*np.pi) * fs
...
>>> fig, (ax0, ax1) = plt.subplots(nrows=2, sharex='all', tight_layout=True)
>>> ax0.set_title("Amplitude-modulated Chirp Signal")
>>> ax0.set_ylabel("Amplitude")
>>> ax0.plot(t, signal, label='Signal')
>>> ax0.plot(t, amplitude_envelope, label='Envelope')
>>> ax0.legend()
>>> ax1.set(xlabel="Time in seconds", ylabel="Phase in rad", ylim=(0, 120))
>>> ax1.plot(t[1:], instantaneous_frequency, 'C2-', label='Instantaneous Phase')
>>> ax1.legend()
>>> plt.show()

../../_images/scipy-signal-hilbert-1.png