scipy.signal.

firls#

scipy.signal.firls(numtaps, bands, desired, *, weight=None, fs=None)[Quelle]#

FIR-Filterdesign mittels Minimierung des Fehlerquadrats.

Berechnet die Filterkoeffizienten für den linearen Phasen-FIR-Filter (Finite Impulse Response), der die beste Approximation der gewünschten Frequenzantwort im Sinne der kleinsten Quadrate aufweist (d. h. das Integral des gewichteten mittleren quadratischen Fehlers innerhalb der spezifizierten Bänder wird minimiert), wie durch bands und desired beschrieben.

Parameter:

numtapsint: Die Anzahl der Taps im FIR-Filter. numtaps muss ungerade sein.
bandsarray_like: Eine monoton nicht abnehmende Sequenz, die die Bandkanten in Hz enthält. Alle Elemente müssen nicht-negativ und kleiner oder gleich der Nyquist-Frequenz sein, die durch nyq gegeben ist. Die Bänder werden als Frequenzpaare angegeben, daher muss seine Länge gerade sein, wenn ein 1D-Array verwendet wird, z. B. np.array([0, 1, 2, 3, 4, 5]). Alternativ können die Bänder als 2D-Array der Größe nx2 angegeben werden, wobei n die Anzahl der Bänder ist, z. B. np.array([[0, 1], [2, 3], [4, 5]]).
desiredarray_like: Eine Sequenz, die die gleiche Größe wie bands hat und den gewünschten Pegel am Start- und Endpunkt jedes Bandes enthält.
weightarray_like, optional: Eine relative Gewichtung, die jedem Bandbereich bei der Lösung des Problems der kleinsten Quadrate zugewiesen wird. weight muss halb so groß sein wie bands.
fsfloat, optional: Die Abtastfrequenz des Signals. Jede Frequenz in bands muss zwischen 0 und fs/2 (einschließlich) liegen. Standard ist 2.

Rückgabe:

coeffsndarray: Koeffizienten des optimalen FIR-Filters (im Sinne der kleinsten Quadrate).

Siehe auch

firwin
firwin2
minimum_phase
remez

Hinweise

Diese Implementierung folgt dem Algorithmus in [1]. Wie dort erwähnt, hat das Design mit kleinsten Quadraten mehrere Vorteile:

Optimal im Sinne der kleinsten Quadrate.

Einfache, nicht-iterative Methode.

Die allgemeine Lösung kann durch Lösung eines linearen Gleichungssystems erhalten werden.

Ermöglicht die Verwendung einer frequenzabhängigen Gewichtungsfunktion.

Diese Funktion konstruiert einen FIR-Filter vom Typ I mit linearem Phasenverhalten, der eine ungerade Anzahl von coeffs enthält, die für \(n < numtaps\) gelten:

\[coeffs(n) = coeffs(numtaps - 1 - n)\]

Die ungerade Anzahl von Koeffizienten und die Filtersymmetrie vermeiden Randbedingungen, die andernfalls an den Nyquist- und 0-Frequenzen auftreten könnten (z. B. bei Varianten Typ II, III oder IV).

Hinzugefügt in Version 0.18.

Referenzen

[1]

Ivan Selesnick, Linear-Phase Fir Filter Design By Least Squares. OpenStax CNX. 9. August 2005. https://eeweb.engineering.nyu.edu/iselesni/EL713/firls/firls.pdf

Beispiele

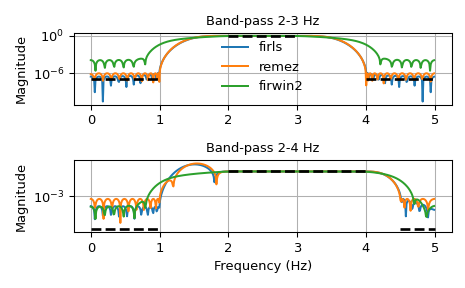
Wir möchten einen Bandpassfilter konstruieren. Beachten Sie, dass das Verhalten in den Frequenzbereichen zwischen unseren Sperrbändern und Durchlassbändern nicht spezifiziert ist und je nach den Parametern unseres Filters überschießen kann.

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> fig, axs = plt.subplots(2)
>>> fs = 10.0  # Hz
>>> desired = (0, 0, 1, 1, 0, 0)
>>> for bi, bands in enumerate(((0, 1, 2, 3, 4, 5), (0, 1, 2, 4, 4.5, 5))):
...     fir_firls = signal.firls(73, bands, desired, fs=fs)
...     fir_remez = signal.remez(73, bands, desired[::2], fs=fs)
...     fir_firwin2 = signal.firwin2(73, bands, desired, fs=fs)
...     hs = list()
...     ax = axs[bi]
...     for fir in (fir_firls, fir_remez, fir_firwin2):
...         freq, response = signal.freqz(fir)
...         hs.append(ax.semilogy(0.5*fs*freq/np.pi, np.abs(response))[0])
...     for band, gains in zip(zip(bands[::2], bands[1::2]),
...                            zip(desired[::2], desired[1::2])):
...         ax.semilogy(band, np.maximum(gains, 1e-7), 'k--', linewidth=2)
...     if bi == 0:
...         ax.legend(hs, ('firls', 'remez', 'firwin2'),
...                   loc='lower center', frameon=False)
...     else:
...         ax.set_xlabel('Frequency (Hz)')
...     ax.grid(True)
...     ax.set(title='Band-pass %d-%d Hz' % bands[2:4], ylabel='Magnitude')
...
>>> fig.tight_layout()
>>> plt.show()