scipy.signal.

freqz_sos#

scipy.signal.freqz_sos(sos, worN=512, whole=False, fs=6.283185307179586)[Quelle]#

Berechnet die Frequenzantwort eines digitalen Filters im SOS-Format.

Gegeben sei sos, ein Array mit der Form (n, 6) von Zweigstellen zweiter Ordnung eines digitalen Filters, berechnen Sie die Frequenzantwort der Systemfunktion

       B0(z)   B1(z)         B{n-1}(z)
H(z) = ----- * ----- * ... * ---------
       A0(z)   A1(z)         A{n-1}(z)

für z = exp(omega*1j), wobei B{k}(z) und A{k}(z) Zähler und Nenner der Übertragungsfunktion des k-ten Zweigstellen zweiter Ordnung sind.

Parameter:

sosarray_like

Array von Koeffizienten von Filtersektionen zweiter Ordnung, muss die Form (n_sections, 6) haben. Jede Zeile entspricht einer Filtersektion zweiter Ordnung, wobei die ersten drei Spalten die Zählerkoeffizienten und die letzten drei die Nennerkoeffizienten liefern.

worN{None, int, array_like}, optional

Wenn eine einzelne Ganzzahl, berechnen Sie dann bei dieser Anzahl von Frequenzen (Standard ist N=512). Die Verwendung einer Zahl, die für FFT-Berechnungen schnell ist, kann zu schnelleren Berechnungen führen (siehe Hinweise zu freqz).

Wenn array_like, berechnen Sie die Antwort bei den gegebenen Frequenzen (muss 1-D sein). Diese sind in denselben Einheiten wie fs.

wholebool, optional

Normalerweise werden Frequenzen von 0 bis zur Nyquist-Frequenz, fs/2 (obere Hälfte des Einheitskreises) berechnet. Wenn whole True ist, berechnen Sie Frequenzen von 0 bis fs.

fsfloat, optional

Die Abtastfrequenz des digitalen Systems. Standardmäßig 2*pi Radiant/Abtastung (also w von 0 bis pi).

Hinzugefügt in Version 1.2.0.

Rückgabe:

wndarray: Die Frequenzen, bei denen h berechnet wurde, in denselben Einheiten wie fs. Standardmäßig wird w auf den Bereich [0, pi) (Radiant/Sample) normalisiert.
hndarray: Die Frequenzantwort als komplexe Zahlen.

Siehe auch

freqz, sosfilt, sosfreqz

Hinweise

Diese Funktion hieß in älteren Versionen (≥ 0.19.0) sosfreqz.

Hinzugefügt in Version 1.15.0.

Beispiele

Entwirft einen Bandpassfilter 15. Ordnung im SOS-Format.

>>> from scipy import signal
>>> import numpy as np
>>> sos = signal.ellip(15, 0.5, 60, (0.2, 0.4), btype='bandpass',
...                    output='sos')

Berechnet die Frequenzantwort bei 1500 Punkten von DC bis Nyquist.

>>> w, h = signal.freqz_sos(sos, worN=1500)

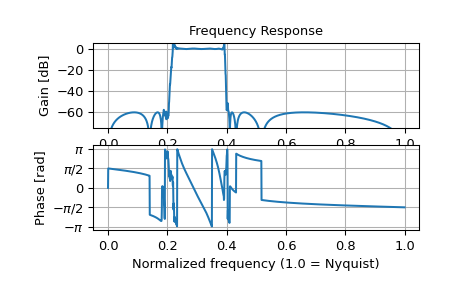
Zeichnet die Antwort.

>>> import matplotlib.pyplot as plt
>>> plt.subplot(2, 1, 1)
>>> db = 20*np.log10(np.maximum(np.abs(h), 1e-5))
>>> plt.plot(w/np.pi, db)
>>> plt.ylim(-75, 5)
>>> plt.grid(True)
>>> plt.yticks([0, -20, -40, -60])
>>> plt.ylabel('Gain [dB]')
>>> plt.title('Frequency Response')
>>> plt.subplot(2, 1, 2)
>>> plt.plot(w/np.pi, np.angle(h))
>>> plt.grid(True)
>>> plt.yticks([-np.pi, -0.5*np.pi, 0, 0.5*np.pi, np.pi],
...            [r'$-\pi$', r'$-\pi/2$', '0', r'$\pi/2$', r'$\pi$'])
>>> plt.ylabel('Phase [rad]')
>>> plt.xlabel('Normalized frequency (1.0 = Nyquist)')
>>> plt.show()

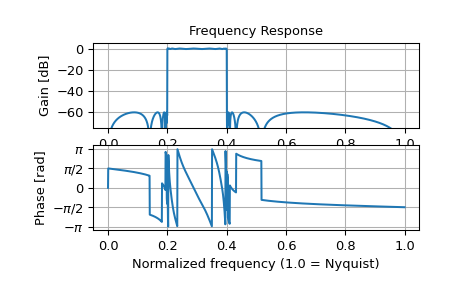
../../_images/scipy-signal-freqz_sos-1_00_00.png

Wenn derselbe Filter als einzelne Übertragungsfunktion implementiert ist, verfälschen numerische Fehler die Frequenzantwort.

>>> b, a = signal.ellip(15, 0.5, 60, (0.2, 0.4), btype='bandpass',
...                    output='ba')
>>> w, h = signal.freqz(b, a, worN=1500)
>>> plt.subplot(2, 1, 1)
>>> db = 20*np.log10(np.maximum(np.abs(h), 1e-5))
>>> plt.plot(w/np.pi, db)
>>> plt.ylim(-75, 5)
>>> plt.grid(True)
>>> plt.yticks([0, -20, -40, -60])
>>> plt.ylabel('Gain [dB]')
>>> plt.title('Frequency Response')
>>> plt.subplot(2, 1, 2)
>>> plt.plot(w/np.pi, np.angle(h))
>>> plt.grid(True)
>>> plt.yticks([-np.pi, -0.5*np.pi, 0, 0.5*np.pi, np.pi],
...            [r'$-\pi$', r'$-\pi/2$', '0', r'$\pi/2$', r'$\pi$'])
>>> plt.ylabel('Phase [rad]')
>>> plt.xlabel('Normalized frequency (1.0 = Nyquist)')
>>> plt.show()

../../_images/scipy-signal-freqz_sos-1_01_00.png