scipy.signal.

sosfilt

scipy.signal.sosfilt(sos, x, axis=-1, zi=None)

Daten entlang einer Dimension mit verketteten Null-Null-Abschnitten filtern.

Filtert eine Datensequenz, x, mit einem digitalen IIR-Filter, der durch sos definiert ist.

Parameter:

sosarray_like

Array von Koeffizienten von Filtersektionen zweiter Ordnung, muss die Form (n_sections, 6) haben. Jede Zeile entspricht einer Filtersektion zweiter Ordnung, wobei die ersten drei Spalten die Zählerkoeffizienten und die letzten drei die Nennerkoeffizienten liefern.

xarray_like

Ein N-dimensionales Eingabearray.

axisint, optional

Die Achse des Eingabedatenarrays, entlang der der lineare Filter angewendet werden soll. Der Filter wird auf jeden Unterarray entlang dieser Achse angewendet. Standard ist -1.

ziarray_like, optional

Anfangsbedingungen für die Verzögerungen des verketteten Filters. Es ist ein (mindestens 2D-)Vektor der Form (n_sections, ..., 2, ...), wobei ..., 2, ... die Form von x bezeichnet, wobei x.shape[axis] durch 2 ersetzt ist. Wenn zi None ist oder nicht angegeben wird, wird eine Anfangsruhe (d.h. alle Nullen) angenommen. Beachten Sie, dass diese Anfangsbedingungen *nicht* dieselben sind wie die Anfangsbedingungen, die von lfiltic oder lfilter_zi angegeben werden.

Rückgabe:

yndarray

Die Ausgabe des digitalen Filters.

zfndarray, optional

Wenn zi None ist, wird dies nicht zurückgegeben. Andernfalls enthält zf die endgültigen Verzögerungswerte des Filters.

Siehe auch

zpk2sos, sos2zpk, sosfilt_zi, sosfiltfilt, freqz_sos

Hinweise

Die Filterfunktion wird als eine Reihe von Null-Null-Filtern mit umgekehrt transponierter Direktform-II-Struktur implementiert. Sie wurde entwickelt, um numerische Präzisionsfehler bei Filtern höherer Ordnung zu minimieren.

Hinzugefügt in Version 0.16.0.

Beispiele

Probieren Sie es in Ihrem Browser aus!

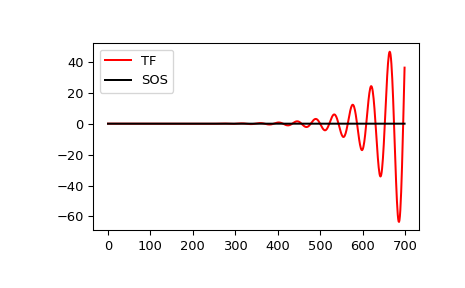
Stellen Sie die Impulsantwort eines 13-ten Ordnung Filters mit lfilter und sosfilt dar und zeigen Sie die Instabilität, die sich aus dem Versuch ergibt, einen Filter 13. Ordnung in einer einzigen Stufe zu realisieren (der numerische Fehler verschiebt einige Pole außerhalb des Einheitskreises).

>>> import matplotlib.pyplot as plt
>>> from scipy import signal
>>> b, a = signal.ellip(13, 0.009, 80, 0.05, output='ba')
>>> sos = signal.ellip(13, 0.009, 80, 0.05, output='sos')
>>> x = signal.unit_impulse(700)
>>> y_tf = signal.lfilter(b, a, x)
>>> y_sos = signal.sosfilt(sos, x)
>>> plt.plot(y_tf, 'r', label='TF')
>>> plt.plot(y_sos, 'k', label='SOS')
>>> plt.legend(loc='best')
>>> plt.show()

ZurückIn Tab öffnen