scipy.signal.

oaconvolve#

scipy.signal.oaconvolve(in1, in2, mode='full', axes=None)[Quelle]#

Faltet zwei N-dimensionale Arrays mithilfe der Überlappungs-Additions-Methode.

Faltet in1 und in2 mithilfe der Überlappungs-Additions-Methode, wobei die Ausgabegröße durch das Argument mode bestimmt wird.

Dies ist im Allgemeinen wesentlich schneller als convolve für große Arrays (n > ~500) und im Allgemeinen wesentlich schneller als fftconvolve, wenn ein Array viel größer ist als das andere, kann jedoch langsamer sein, wenn nur wenige Ausgabewerte benötigt werden oder wenn die Arrays sich in ihrer Form sehr ähnlich sind. Es können nur Float-Arrays ausgegeben werden (Integer- oder Objektdatentyp-Eingaben werden nach Float konvertiert).

Parameter:

in1array_like

Erster Input.

in2array_like

Zweiter Input. Sollte dieselbe Anzahl von Dimensionen wie in1 haben.

modestr {‘full’, ‘valid’, ‘same’}, optional

Ein String, der die Größe der Ausgabe angibt

full: Die Ausgabe ist die vollständige diskrete lineare Faltung der Eingaben. (Standard)
valid: Die Ausgabe besteht nur aus den Elementen, die nicht von der Null-Pufferung abhängen. Im Modus 'valid' muss entweder in1 oder in2 in jeder Dimension mindestens so groß sein wie der andere.
same: Die Ausgabe hat die gleiche Größe wie in1 und ist zentriert bezüglich der 'full'-Ausgabe.

axesint oder Array-ähnlich von ints oder None, optional

Achsen, über die die Faltung berechnet wird. Standardmäßig werden alle Achsen verwendet.

Rückgabe:

outarray: Ein N-dimensionales Array, das einen Teil der diskreten linearen Faltung von in1 mit in2 enthält.

Siehe auch

convolve: Verwendet den direkten Faltungs- oder FFT-Faltungsalgorithmus, je nachdem, welcher schneller ist.
fftconvolve: Eine Implementierung der Faltung mittels FFT.

Hinweise

Hinzugefügt in Version 1.4.0.

Referenzen

[1]

Wikipedia, „Overlap-add_method“. https://en.wikipedia.org/wiki/Overlap-add_method

[2]

Richard G. Lyons. Understanding Digital Signal Processing, Third Edition, 2011. Kapitel 13.10. ISBN 13: 978-0137-02741-5

Beispiele

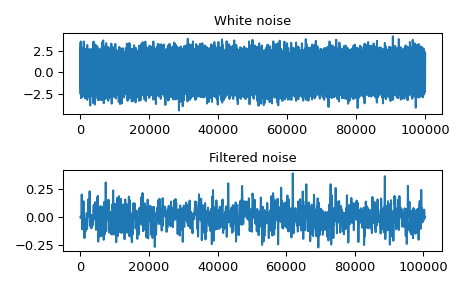
Faltet ein Signal mit 100.000 Samples mit einem Filter mit 512 Samples.

>>> import numpy as np
>>> from scipy import signal
>>> rng = np.random.default_rng()
>>> sig = rng.standard_normal(100000)
>>> filt = signal.firwin(512, 0.01)
>>> fsig = signal.oaconvolve(sig, filt)

>>> import matplotlib.pyplot as plt
>>> fig, (ax_orig, ax_mag) = plt.subplots(2, 1)
>>> ax_orig.plot(sig)
>>> ax_orig.set_title('White noise')
>>> ax_mag.plot(fsig)
>>> ax_mag.set_title('Filtered noise')
>>> fig.tight_layout()
>>> fig.show()

../../_images/scipy-signal-oaconvolve-1.png