scipy.signal.

convolve#

scipy.signal.convolve(in1, in2, mode='full', method='auto')[Quelle]#

Führen Sie die Faltung von zwei N-dimensionalen Arrays durch.

Falten Sie in1 und in2, wobei die Ausgabegröße durch das Argument mode bestimmt wird.

Parameter:

in1array_like

Erster Input.

in2array_like

Zweiter Input. Sollte dieselbe Anzahl von Dimensionen wie in1 haben.

modestr {‘full’, ‘valid’, ‘same’}, optional

Ein String, der die Größe der Ausgabe angibt

full: Die Ausgabe ist die vollständige diskrete lineare Faltung der Eingaben. (Standard)
valid: Die Ausgabe besteht nur aus den Elementen, die nicht von der Null-Pufferung abhängen. Im Modus 'valid' muss entweder in1 oder in2 in jeder Dimension mindestens so groß sein wie der andere.
same: Die Ausgabe hat die gleiche Größe wie in1 und ist zentriert bezüglich der 'full'-Ausgabe.

methodstr {‘auto’, ‘direct’, ‘fft’}, optional

Eine Zeichenkette, die angibt, welche Methode zur Berechnung der Faltung verwendet werden soll.

direct: Die Faltung wird direkt aus Summen bestimmt, der Definition der Faltung.
fft: Die Fourier-Transformation wird verwendet, um die Faltung durch Aufruf von fftconvolve durchzuführen.
auto: Wählt automatisch die direkte oder die Fourier-Methode basierend auf einer Schätzung, welche schneller ist (Standard). Siehe Hinweise für weitere Details.

Hinzugefügt in Version 0.19.0.

Rückgabe:

convolvearray: Ein N-dimensionales Array, das einen Teil der diskreten linearen Faltung von in1 mit in2 enthält.

Warnungen:

RuntimeWarning: Die Verwendung der FFT-Faltung für Eingaben, die NAN oder INF enthalten, führt dazu, dass die gesamte Ausgabe NAN oder INF ist. Verwenden Sie method='direct', wenn Ihre Eingabe NAN- oder INF-Werte enthält.

Siehe auch

numpy.polymul: führt Polynommultiplikation durch (gleiche Operation, akzeptiert aber auch poly1d-Objekte)
choose_conv_method: wählt die schnellste geeignete Faltungsmethode aus
fftconvolve: Verwendet immer die FFT-Methode.
oaconvolve: Verwendet die Overlap-Add-Methode zur Faltung, die im Allgemeinen schneller ist, wenn die Eingabearrays groß und signifikant unterschiedlich in der Größe sind.

Hinweise

Standardmäßig verwenden convolve und correlate method='auto', was choose_conv_method aufruft, um die schnellste Methode anhand vorab berechneter Werte auszuwählen (choose_conv_method kann auch reale Zeitmessungen mit einem Schlüsselwortargument durchführen). Da fftconvolve auf Gleitkommazahlen angewiesen ist, gibt es bestimmte Einschränkungen, die method='direct' erzwingen können (mehr Details in der Dokumentation von choose_conv_method).

Beispiele

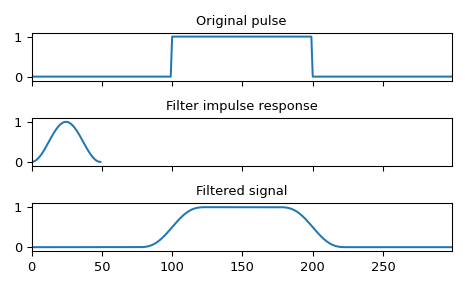
Glatten eines Rechteckimpulses mit einem Hann-Fenster

>>> import numpy as np
>>> from scipy import signal
>>> sig = np.repeat([0., 1., 0.], 100)
>>> win = signal.windows.hann(50)
>>> filtered = signal.convolve(sig, win, mode='same') / sum(win)

>>> import matplotlib.pyplot as plt
>>> fig, (ax_orig, ax_win, ax_filt) = plt.subplots(3, 1, sharex=True)
>>> ax_orig.plot(sig)
>>> ax_orig.set_title('Original pulse')
>>> ax_orig.margins(0, 0.1)
>>> ax_win.plot(win)
>>> ax_win.set_title('Filter impulse response')
>>> ax_win.margins(0, 0.1)
>>> ax_filt.plot(filtered)
>>> ax_filt.set_title('Filtered signal')
>>> ax_filt.margins(0, 0.1)
>>> fig.tight_layout()
>>> fig.show()

../../_images/scipy-signal-convolve-1.png