scipy.signal.

sweep_poly#

scipy.signal.sweep_poly(t, poly, phi=0)[Quelle]#

Frequenz-Sweep-Cosinus-Generator mit zeitabhängiger Frequenz.

Diese Funktion erzeugt eine sinusförmige Funktion, deren momentane Frequenz sich mit der Zeit ändert. Die Frequenz zum Zeitpunkt t wird durch das Polynom poly gegeben.

Parameter:

tndarray

Zeitpunkte, zu denen die Wellenform ausgewertet werden soll.

poly1-D array_like oder Instanz von numpy.poly1d

Die gewünschte Frequenz, ausgedrückt als Polynom. Wenn poly eine Liste oder ein ndarray der Länge n ist, dann sind die Elemente von poly die Koeffizienten des Polynoms und die momentane Frequenz ist

f(t) = poly[0]*t**(n-1) + poly[1]*t**(n-2) + ... + poly[n-1]

Wenn poly eine Instanz von numpy.poly1d ist, dann ist die momentane Frequenz

f(t) = poly(t)

phifloat, optional

Phasenverschiebung in Grad, Standard: 0.

Rückgabe:

sweep_polyndarray: Ein Numpy-Array, das das Signal enthält, das zu t mit der angeforderten zeitvariablen Frequenz ausgewertet wurde. Genauer gesagt gibt die Funktion cos(phase + (pi/180)*phi) zurück, wobei phase das Integral (von 0 bis t) von 2 * pi * f(t) ist; f(t) ist wie oben definiert.

Siehe auch

chirp

Hinweise

Hinzugefügt in Version 0.8.0.

Wenn poly eine Liste oder ein ndarray der Länge n ist, dann sind die Elemente von poly die Koeffizienten des Polynoms und die momentane Frequenz ist

f(t) = poly[0]*t**(n-1) + poly[1]*t**(n-2) + ... + poly[n-1]

Wenn poly eine Instanz von numpy.poly1d ist, dann ist die momentane Frequenz

f(t) = poly(t)

Schließlich ist die Ausgabe s

cos(phase + (pi/180)*phi)

wobei phase das Integral von 0 bis t von 2 * pi * f(t) ist, f(t) wie oben definiert.

Beispiele

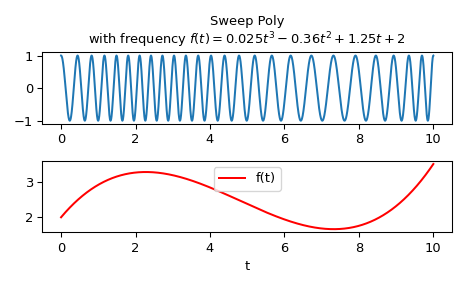
Berechnet die Wellenform mit der momentanen Frequenz

f(t) = 0.025*t**3 - 0.36*t**2 + 1.25*t + 2

über das Intervall 0 <= t <= 10.

>>> import numpy as np
>>> from scipy.signal import sweep_poly
>>> p = np.poly1d([0.025, -0.36, 1.25, 2.0])
>>> t = np.linspace(0, 10, 5001)
>>> w = sweep_poly(t, p)

Zeichne sie

>>> import matplotlib.pyplot as plt
>>> plt.subplot(2, 1, 1)
>>> plt.plot(t, w)
>>> plt.title("Sweep Poly\nwith frequency " +
...           "$f(t) = 0.025t^3 - 0.36t^2 + 1.25t + 2$")
>>> plt.subplot(2, 1, 2)
>>> plt.plot(t, p(t), 'r', label='f(t)')
>>> plt.legend()
>>> plt.xlabel('t')
>>> plt.tight_layout()
>>> plt.show()

../../_images/scipy-signal-sweep_poly-1.png