scipy.signal.windows.

dpss

scipy.signal.windows.dpss(M, NW, Kmax=None, sym=True, norm=None, return_ratios=False, *, xp=None, device=None)

Berechnet die diskreten sphärisch-prolaten Sequenzen (DPSS).

DPSS (oder Slepian-Sequenzen) werden oft in der Multitaper-Schätzung der Leistungsdichtespektrums verwendet (siehe [1]). Das erste Fenster in der Sequenz kann verwendet werden, um die Energiekonzentration im Hauptkeulen zu maximieren, und wird auch als Slepian-Fenster bezeichnet.

Parameter:

Mint

Fensterlänge.

NWfloat

Standardisierte halbe Bandbreite, entsprechend 2*NW = BW/f0 = BW*M*dt, wobei dt als 1 angenommen wird.

Kmaxint | None, optional

Anzahl der zurückzugebenden DPSS-Fenster (Ordnungen 0 bis Kmax-1). Wenn None (Standard), wird nur ein einzelnes Fenster der Form (M,) anstelle eines Arrays von Fenstern der Form (Kmax, M) zurückgegeben.

symbool, optional

Wenn True (Standard), wird ein symmetrisches Fenster zur Filterentwurf verwendet. Wenn False, wird ein periodisches Fenster für die Spektralanalyse generiert.

norm{2, ‘approximate’, ‘subsample’} | None, optional

Wenn ‘approximate’ oder ‘subsample’, dann werden die Fenster nach ihrem Maximalwert normalisiert, und ein Korrekturfaktor für Fenster mit gerader Länge wird entweder mit M**2/(M**2+NW) (“approximate”) oder einer FFT-basierten Subsampelverschiebung (“subsample”) angewendet, siehe Hinweise für Details. Wenn None, dann wird “approximate” verwendet, wenn Kmax=None ist, andernfalls 2 (was der l2-Norm entspricht).

return_ratiosbool, optional

Wenn True, werden zusätzlich zu den Fenstern auch die Konzentrationsverhältnisse zurückgegeben.

xparray_namespace, optional

Optionaler Array-Namespace. Sollte mit dem Array-API-Standard kompatibel sein oder von array-api-compat unterstützt werden. Standard: numpy

device: any

optionale Gerätespezifikation für die Ausgabe. Sollte mit einer der unterstützten Gerätespezifikationen in xp übereinstimmen.

Rückgabe:

vndarray, shape (Kmax, M) oder (M,)

Die DPSS-Fenster. Ist 1D, wenn Kmax None ist.

rndarray, shape (Kmax,) oder float, optional

Die Konzentrationsverhältnisse für die Fenster. Wird nur zurückgegeben, wenn return_ratios True ergibt. Ist 0D, wenn Kmax None ist.

Hinweise

Diese Berechnung verwendet die in [2] angegebene tridiagonale Eigenvektorformulierung.

Die Standardnormalisierung für Kmax=None, d.h. im Fenstermodus, die einfache l-unendlich-Norm würde zwei Einheitswerte erzeugen, was zu leichten Normalisierungsunterschieden zwischen geraden und ungeraden Ordnungen führt. Die ungefähre Korrektur von M**2/float(M**2+NW) für gerade Stichprobennummern wird verwendet, um diesen Effekt auszugleichen (siehe Beispiele unten).

Für sehr lange Signale (z.B. 1e6 Elemente) kann es nützlich sein, Fenster zu berechnen, die um Größenordnungen kürzer sind, und Interpolation (z.B. scipy.interpolate.interp1d) zu verwenden, um Taper der Länge M zu erhalten, aber dies erhält im Allgemeinen nicht die Orthogonalität zwischen den Taper.

Hinzugefügt in Version 1.1.

Referenzen

[1]

Percival DB, Walden WT. Spectral Analysis for Physical Applications: Multitaper and Conventional Univariate Techniques. Cambridge University Press; 1993.

[2]

Slepian, D. Prolate spheroidal wave functions, Fourier analysis, and uncertainty V: The discrete case. Bell System Technical Journal, Volume 57 (1978), 1371430.

[3]

Kaiser, JF, Schafer RW. On the Use of the I0-Sinh Window for Spectrum Analysis. IEEE Transactions on Acoustics, Speech and Signal Processing. ASSP-28 (1): 105-107; 1980.

Beispiele

Probieren Sie es in Ihrem Browser aus!

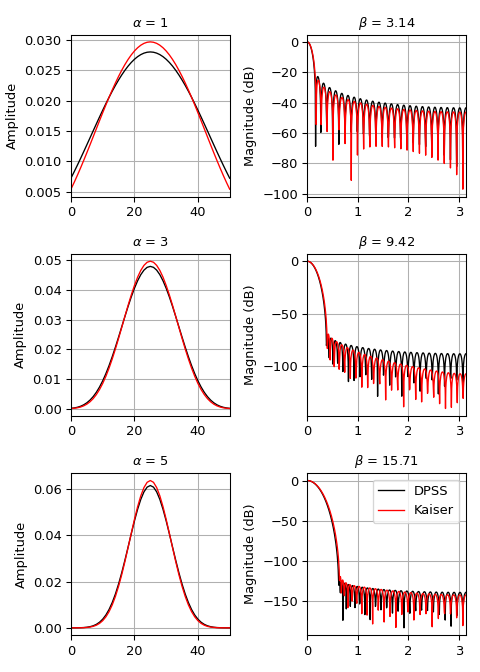
Wir können das Fenster mit kaiser vergleichen, das als einfach zu berechnende Alternative erfunden wurde [3] (Beispiel adaptiert von hier)

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import windows, freqz
>>> M = 51
>>> fig, axes = plt.subplots(3, 2, figsize=(5, 7))
>>> for ai, alpha in enumerate((1, 3, 5)):
...     win_dpss = windows.dpss(M, alpha)
...     beta = alpha*np.pi
...     win_kaiser = windows.kaiser(M, beta)
...     for win, c in ((win_dpss, 'k'), (win_kaiser, 'r')):
...         win /= win.sum()
...         axes[ai, 0].plot(win, color=c, lw=1.)
...         axes[ai, 0].set(xlim=[0, M-1], title=rf'$\alpha$ = {alpha}',
...                         ylabel='Amplitude')
...         w, h = freqz(win)
...         axes[ai, 1].plot(w, 20 * np.log10(np.abs(h)), color=c, lw=1.)
...         axes[ai, 1].set(xlim=[0, np.pi],
...                         title=rf'$\beta$ = {beta:0.2f}',
...                         ylabel='Magnitude (dB)')
>>> for ax in axes.ravel():
...     ax.grid(True)
>>> axes[2, 1].legend(['DPSS', 'Kaiser'])
>>> fig.tight_layout()
>>> plt.show()

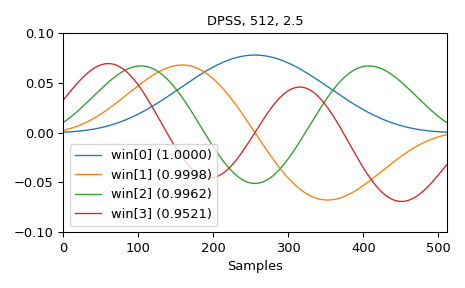
Und hier sind Beispiele der ersten vier Fenster zusammen mit ihren Konzentrationsverhältnissen

>>> M = 512
>>> NW = 2.5
>>> win, eigvals = windows.dpss(M, NW, 4, return_ratios=True)
>>> fig, ax = plt.subplots(1)
>>> ax.plot(win.T, linewidth=1.)
>>> ax.set(xlim=[0, M-1], ylim=[-0.1, 0.1], xlabel='Samples',
...        title=f'DPSS, {M:d}, {NW:0.1f}')
>>> ax.legend([f'win[{ii}] ({ratio:0.4f})'
...            for ii, ratio in enumerate(eigvals)])
>>> fig.tight_layout()
>>> plt.show()

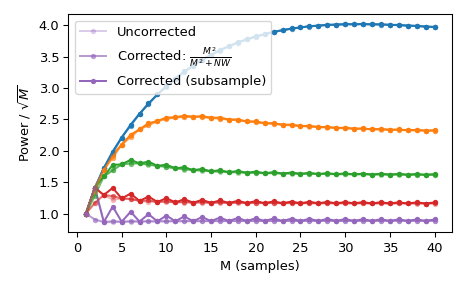
Die Verwendung einer Standard- \(l_{\infty}\)-Norm würde für gerade M zwei Einheitswerte ergeben, aber nur einen Einheitswert für ungerade M. Dies führt zu ungleichmäßiger Fensterleistung, die durch die ungefähre Korrektur M**2/float(M**2+NW) ausgeglichen werden kann, die durch die Verwendung von norm='approximate' ausgewählt werden kann (was dasselbe ist wie norm=None, wenn Kmax=None ist, wie hier der Fall). Alternativ kann die langsamere Option norm='subsample' verwendet werden, die eine Subsampelverschiebung im Frequenzbereich (FFT) zur Berechnung der Korrektur verwendet.

>>> Ms = np.arange(1, 41)
>>> factors = (50, 20, 10, 5, 2.0001)
>>> energy = np.empty((3, len(Ms), len(factors)))
>>> for mi, M in enumerate(Ms):
...     for fi, factor in enumerate(factors):
...         NW = M / float(factor)
...         # Corrected using empirical approximation (default)
...         win = windows.dpss(M, NW)
...         energy[0, mi, fi] = np.sum(win ** 2) / np.sqrt(M)
...         # Corrected using subsample shifting
...         win = windows.dpss(M, NW, norm='subsample')
...         energy[1, mi, fi] = np.sum(win ** 2) / np.sqrt(M)
...         # Uncorrected (using l-infinity norm)
...         win /= win.max()
...         energy[2, mi, fi] = np.sum(win ** 2) / np.sqrt(M)
>>> fig, ax = plt.subplots(1)
>>> hs = ax.plot(Ms, energy[2], '-o', markersize=4,
...              markeredgecolor='none')
>>> leg = [hs[-1]]
>>> for hi, hh in enumerate(hs):
...     h1 = ax.plot(Ms, energy[0, :, hi], '-o', markersize=4,
...                  color=hh.get_color(), markeredgecolor='none',
...                  alpha=0.66)
...     h2 = ax.plot(Ms, energy[1, :, hi], '-o', markersize=4,
...                  color=hh.get_color(), markeredgecolor='none',
...                  alpha=0.33)
...     if hi == len(hs) - 1:
...         leg.insert(0, h1[0])
...         leg.insert(0, h2[0])
>>> ax.set(xlabel='M (samples)', ylabel=r'Power / $\sqrt{M}$')
>>> ax.legend(leg, ['Uncorrected', r'Corrected: $\frac{M^2}{M^2+NW}$',
...                 'Corrected (subsample)'])
>>> fig.tight_layout()

ZurückIn Tab öffnen