scipy.special.airy#

scipy.special.airy(z, out=None) = <ufunc 'airy'>#

Airy-Funktionen und ihre Ableitungen.

Parameter:

zarray_like: Reeller oder komplexer Argument.
outtuple von ndarray, optional: Optionale Ausgabe-Arrays für die Funktionswerte

Rückgabe:

Ai, Aip, Bi, Bip4-Tupel aus Skalar oder ndarray: Airy-Funktionen Ai und Bi sowie ihre Ableitungen Aip und Bip.

Siehe auch

airye: exponentiell skalierte Airy-Funktionen.

Hinweise

Die Airy-Funktionen Ai und Bi sind zwei unabhängige Lösungen von

\[y''(x) = x y(x).\]

Für reelles z im Bereich [-10, 10] wird die Berechnung durch Aufruf der Cephes [1] airy-Routine durchgeführt, die Potenzreihensummation für kleine z und rationale Minimax-Approximationen für große z verwendet.

Außerhalb dieses Bereichs werden die AMOS [2] zairy und zbiry Routinen verwendet. Sie werden mittels Potenzreihen für \(|z| < 1\) und den folgenden Beziehungen zu modifizierten Bessel-Funktionen für größere z berechnet (wobei \(t \equiv 2 z^{3/2}/3\))

\[ \begin{align}\begin{aligned}Ai(z) = \frac{1}{\pi \sqrt{3}} K_{1/3}(t)\\Ai'(z) = -\frac{z}{\pi \sqrt{3}} K_{2/3}(t)\\Bi(z) = \sqrt{\frac{z}{3}} \left(I_{-1/3}(t) + I_{1/3}(t) \right)\\Bi'(z) = \frac{z}{\sqrt{3}} \left(I_{-2/3}(t) + I_{2/3}(t)\right)\end{aligned}\end{align} \]

Referenzen

[1]

Cephes Mathematical Functions Library, http://www.netlib.org/cephes/

[2]

Donald E. Amos, „AMOS, A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order“, http://netlib.org/amos/

Beispiele

Berechnen Sie die Airy-Funktionen auf dem Intervall [-15, 5].

>>> import numpy as np
>>> from scipy import special
>>> x = np.linspace(-15, 5, 201)
>>> ai, aip, bi, bip = special.airy(x)

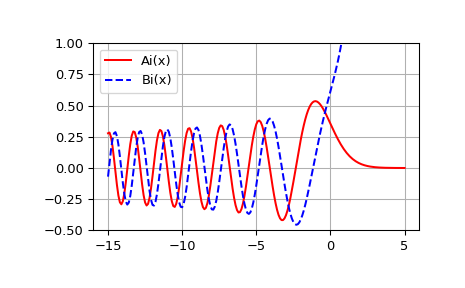
Plotten Sie Ai(x) und Bi(x).

>>> import matplotlib.pyplot as plt
>>> plt.plot(x, ai, 'r', label='Ai(x)')
>>> plt.plot(x, bi, 'b--', label='Bi(x)')
>>> plt.ylim(-0.5, 1.0)
>>> plt.grid()
>>> plt.legend(loc='upper left')
>>> plt.show()