scipy.special.kolmogorov#

scipy.special.kolmogorov(y, out=None) = <ufunc 'kolmogorov'>#

Komplementäre Verteilungsfunktion (Survival Function) der Kolmogorov-Verteilung.

Gibt die komplementäre Verteilungsfunktion von Kolmogoroffs Grenzverteilung zurück (D_n*\sqrt(n) für n gegen unendlich) eines zweiseitigen Tests auf Gleichheit zwischen einer empirischen und einer theoretischen Verteilung. Sie ist gleich der (Grenze für n gegen unendlich der) Wahrscheinlichkeit, dass sqrt(n) * max absolute deviation > y.

Parameter:

yfloat array_like: Absolute Abweichung zwischen der empirischen kumulativen Verteilungsfunktion (ECDF) und der Ziel-CDF, multipliziert mit sqrt(n).
outndarray, optional: Optionales Ausgabe-Array für die Funktionsergebnisse

Rückgabe:

skalar oder ndarray: Die Werte von kolmogorov(y)

Siehe auch

kolmogi: Die Inverse Survival Function für die Verteilung
scipy.stats.kstwobign: Bietet die Funktionalität als kontinuierliche Verteilung
smirnov, smirnovi: Funktionen für die einseitige Verteilung

Hinweise

kolmogorov wird von stats.kstest bei der Anwendung des Kolmogorov-Smirnov-Anpassungstests verwendet. Aus historischen Gründen ist diese Funktion in scipy.special verfügbar, aber der empfohlene Weg, die genauesten CDF/SF/PDF/PPF/ISF-Berechnungen zu erzielen, ist die Verwendung der stats.kstwobign-Verteilung.

Beispiele

Zeigt die Wahrscheinlichkeit einer Lücke von mindestens 0, 0,5 und 1,0.

>>> import numpy as np
>>> from scipy.special import kolmogorov
>>> from scipy.stats import kstwobign
>>> kolmogorov([0, 0.5, 1.0])
array([ 1.        ,  0.96394524,  0.26999967])

Vergleicht eine Stichprobe der Größe 1000, gezogen aus einer Laplace(0, 1)-Verteilung, mit der Zielverteilung, einer Normal(0, 1)-Verteilung.

>>> from scipy.stats import norm, laplace
>>> rng = np.random.default_rng()
>>> n = 1000
>>> lap01 = laplace(0, 1)
>>> x = np.sort(lap01.rvs(n, random_state=rng))
>>> np.mean(x), np.std(x)
(-0.05841730131499543, 1.3968109101997568)

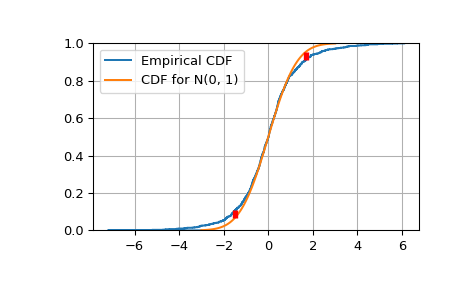
Konstruiert die empirische kumulative Verteilungsfunktion und die K-S-Statistik Dn.

>>> target = norm(0,1)  # Normal mean 0, stddev 1
>>> cdfs = target.cdf(x)
>>> ecdfs = np.arange(n+1, dtype=float)/n
>>> gaps = np.column_stack([cdfs - ecdfs[:n], ecdfs[1:] - cdfs])
>>> Dn = np.max(gaps)
>>> Kn = np.sqrt(n) * Dn
>>> print('Dn=%f, sqrt(n)*Dn=%f' % (Dn, Kn))
Dn=0.043363, sqrt(n)*Dn=1.371265
>>> print(chr(10).join(['For a sample of size n drawn from a N(0, 1) distribution:',
...   ' the approximate Kolmogorov probability that sqrt(n)*Dn>=%f is %f' %
...    (Kn, kolmogorov(Kn)),
...   ' the approximate Kolmogorov probability that sqrt(n)*Dn<=%f is %f' %
...    (Kn, kstwobign.cdf(Kn))]))
For a sample of size n drawn from a N(0, 1) distribution:
 the approximate Kolmogorov probability that sqrt(n)*Dn>=1.371265 is 0.046533
 the approximate Kolmogorov probability that sqrt(n)*Dn<=1.371265 is 0.953467

Plottet die empirische kumulative Verteilungsfunktion gegen die Ziel-N(0, 1)-CDF.

>>> import matplotlib.pyplot as plt
>>> plt.step(np.concatenate([[-3], x]), ecdfs, where='post', label='Empirical CDF')
>>> x3 = np.linspace(-3, 3, 100)
>>> plt.plot(x3, target.cdf(x3), label='CDF for N(0, 1)')
>>> plt.ylim([0, 1]); plt.grid(True); plt.legend();
>>> # Add vertical lines marking Dn+ and Dn-
>>> iminus, iplus = np.argmax(gaps, axis=0)
>>> plt.vlines([x[iminus]], ecdfs[iminus], cdfs[iminus],
...            color='r', linestyle='dashed', lw=4)
>>> plt.vlines([x[iplus]], cdfs[iplus], ecdfs[iplus+1],
...            color='r', linestyle='dashed', lw=4)
>>> plt.show()

../../_images/scipy-special-kolmogorov-1.png