scipy.special.smirnov#

scipy.special.smirnov(n, d, out=None) = <ufunc 'smirnov'>#

Kolmogorov-Smirnov komplementäre kumulative Verteilungsfunktion

Gibt die exakte Kolmogorov-Smirnov komplementäre kumulative Verteilungsfunktion (auch Überlebensfunktion) von Dn+ (oder Dn-) für einen einseitigen Test der Gleichheit zwischen einer empirischen und einer theoretischen Verteilung zurück. Sie ist gleich der Wahrscheinlichkeit, dass die maximale Differenz zwischen einer theoretischen Verteilung und einer empirischen, basierend auf n Stichproben, größer als d ist.

Parameter:

nint: Anzahl der Stichproben
dfloat array_like: Abweichung zwischen der empirischen CDF (ECDF) und der Ziel-CDF.
outndarray, optional: Optionales Ausgabe-Array für die Funktionsergebnisse

Rückgabe:

skalar oder ndarray: Die Werte von smirnov(n, d), Prob(Dn+ >= d) (auch Prob(Dn- >= d))

Siehe auch

smirnovi: Die inverse Überlebensfunktion für die Verteilung
scipy.stats.ksone: Bietet die Funktionalität als kontinuierliche Verteilung
kolmogorov, kolmogi: Funktionen für die zweiseitige Verteilung

Hinweise

smirnov wird von stats.kstest bei der Anwendung des Kolmogorov-Smirnov Güte-Anpassungs-Tests verwendet. Aus historischen Gründen ist diese Funktion in scpy.special verfügbar, aber der empfohlene Weg für die genauesten CDF/SF/PDF/PPF/ISF-Berechnungen ist die Verwendung der stats.ksone Verteilung.

Beispiele

>>> import numpy as np
>>> from scipy.special import smirnov
>>> from scipy.stats import norm

Zeigen Sie die Wahrscheinlichkeit einer Lücke von mindestens 0, 0,5 und 1,0 für eine Stichprobengröße von 5.

>>> smirnov(5, [0, 0.5, 1.0])
array([ 1.   ,  0.056,  0.   ])

Vergleichen Sie eine Stichprobe der Größe 5 mit N(0, 1), der Standardnormalverteilung mit Mittelwert 0 und Standardabweichung 1.

x ist die Stichprobe.

>>> x = np.array([-1.392, -0.135, 0.114, 0.190, 1.82])

>>> target = norm(0, 1)
>>> cdfs = target.cdf(x)
>>> cdfs
array([0.0819612 , 0.44630594, 0.5453811 , 0.57534543, 0.9656205 ])

Konstruieren Sie die empirische CDF und die K-S-Statistiken (Dn+, Dn-, Dn).

>>> n = len(x)
>>> ecdfs = np.arange(n+1, dtype=float)/n
>>> cols = np.column_stack([x, ecdfs[1:], cdfs, cdfs - ecdfs[:n],
...                        ecdfs[1:] - cdfs])
>>> with np.printoptions(precision=3):
...    print(cols)
[[-1.392  0.2    0.082  0.082  0.118]
 [-0.135  0.4    0.446  0.246 -0.046]
 [ 0.114  0.6    0.545  0.145  0.055]
 [ 0.19   0.8    0.575 -0.025  0.225]
 [ 1.82   1.     0.966  0.166  0.034]]
>>> gaps = cols[:, -2:]
>>> Dnpm = np.max(gaps, axis=0)
>>> print(f'Dn-={Dnpm[0]:f}, Dn+={Dnpm[1]:f}')
Dn-=0.246306, Dn+=0.224655
>>> probs = smirnov(n, Dnpm)
>>> print(f'For a sample of size {n} drawn from N(0, 1):',
...       f' Smirnov n={n}: Prob(Dn- >= {Dnpm[0]:f}) = {probs[0]:.4f}',
...       f' Smirnov n={n}: Prob(Dn+ >= {Dnpm[1]:f}) = {probs[1]:.4f}',
...       sep='\n')
For a sample of size 5 drawn from N(0, 1):
 Smirnov n=5: Prob(Dn- >= 0.246306) = 0.4711
 Smirnov n=5: Prob(Dn+ >= 0.224655) = 0.5245

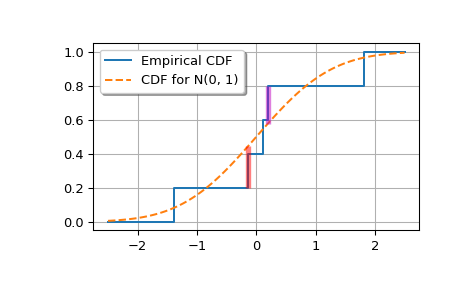
Plotten Sie die empirische CDF und die Standard-Normal-CDF.

>>> import matplotlib.pyplot as plt
>>> plt.step(np.concatenate(([-2.5], x, [2.5])),
...          np.concatenate((ecdfs, [1])),
...          where='post', label='Empirical CDF')
>>> xx = np.linspace(-2.5, 2.5, 100)
>>> plt.plot(xx, target.cdf(xx), '--', label='CDF for N(0, 1)')

Fügen Sie vertikale Linien hinzu, die Dn+ und Dn- markieren.

>>> iminus, iplus = np.argmax(gaps, axis=0)
>>> plt.vlines([x[iminus]], ecdfs[iminus], cdfs[iminus], color='r',
...            alpha=0.5, lw=4)
>>> plt.vlines([x[iplus]], cdfs[iplus], ecdfs[iplus+1], color='m',
...            alpha=0.5, lw=4)

>>> plt.grid(True)
>>> plt.legend(framealpha=1, shadow=True)
>>> plt.show()

../../_images/scipy-special-smirnov-1.png