boxcox_normmax#
- scipy.stats.boxcox_normmax(x, brack=None, method='pearsonr', optimizer=None, *, ymax=BIG_FLOAT)[Quelle]#
Berechnet den optimalen Box-Cox-Transformationsparameter für Eingabedaten.
- Parameter:
- xarray_like
Eingabearray. Alle Einträge müssen positive, endliche, reelle Zahlen sein.
- brack2-Tupel, optional, Standard: (-2.0, 2.0)
Das Startintervall für eine abwärtsgerichtete Klammersuche für den Standard-Solver optimize.brent. Beachten Sie, dass dies in den meisten Fällen nicht kritisch ist; das Endergebnis darf außerhalb dieser Klammer liegen. Wenn optimizer übergeben wird, muss brack None sein.
- methodstr, optional
Die Methode zur Bestimmung des optimalen Transformationsparameters (Parameter
lmbdavonboxcox). Optionen sind- ‘pearsonr’ (Standard)
Maximiert den Pearson-Korrelationskoeffizienten zwischen
y = boxcox(x)und den erwarteten Werten füry, wenn x normalverteilt wäre.- ‘mle’
Maximiert die Log-Likelihood
boxcox_llf. Dies ist die Methode, die inboxcoxverwendet wird.- ‘all’
Verwendet alle verfügbaren Optimierungsmethoden und gibt alle Ergebnisse zurück. Nützlich zum Vergleichen verschiedener Methoden.
- optimizeraufrufbar, optional
optimizer ist eine aufrufbare Funktion, die ein Argument akzeptiert
- funcallable
Die zu minimierende Zielfunktion. fun akzeptiert ein Argument, den Box-Cox-Transformationsparameter lmbda, und gibt den Wert der Funktion (z. B. die negative Log-Likelihood) am angegebenen Argument zurück. Die Aufgabe von optimizer besteht darin, den Wert von lmbda zu finden, der fun *minimiert*.
und gibt ein Objekt zurück, z. B. eine Instanz von
scipy.optimize.OptimizeResult, das den optimalen Wert von lmbda in einem Attribut x enthält.Siehe das folgende Beispiel oder die Dokumentation von
scipy.optimize.minimize_scalarfür weitere Informationen.- ymaxfloat, optional
Der unbeschränkte optimale Transformationsparameter kann dazu führen, dass die Box-Cox-transformierten Daten extreme Größenordnungen aufweisen oder sogar überlaufen. Dieser Parameter beschränkt die MLE-Optimierung so, dass die Größe des transformierten x ymax nicht überschreitet. Der Standardwert ist der maximale Wert des Eingabe-Datentyps. Wenn er auf unendlich gesetzt wird, gibt
boxcox_normmaxden unbeschränkten optimalen Lambda-Wert zurück. Wird ignoriert, wennmethod='pearsonr'.
- Rückgabe:
- maxlogfloat oder ndarray
Der gefundene optimale Transformationsparameter. Ein Array anstelle eines Skalars für
method='all'.
Siehe auch
Beispiele
>>> import numpy as np >>> from scipy import stats >>> import matplotlib.pyplot as plt
Wir können einige Daten generieren und den optimalen
lmbdaauf verschiedene Arten bestimmen>>> rng = np.random.default_rng() >>> x = stats.loggamma.rvs(5, size=30, random_state=rng) + 5 >>> y, lmax_mle = stats.boxcox(x) >>> lmax_pearsonr = stats.boxcox_normmax(x)
>>> lmax_mle 2.217563431465757 >>> lmax_pearsonr 2.238318660200961 >>> stats.boxcox_normmax(x, method='all') array([2.23831866, 2.21756343])
>>> fig = plt.figure() >>> ax = fig.add_subplot(111) >>> prob = stats.boxcox_normplot(x, -10, 10, plot=ax) >>> ax.axvline(lmax_mle, color='r') >>> ax.axvline(lmax_pearsonr, color='g', ls='--')
>>> plt.show()
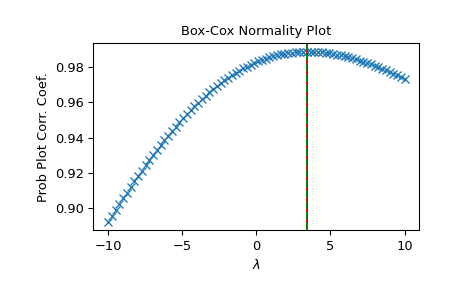
Alternativ können wir unsere eigene optimizer-Funktion definieren. Angenommen, wir sind nur an Werten von lmbda im Intervall [6, 7] interessiert, wir möchten
scipy.optimize.minimize_scalarmitmethod='bounded'verwenden, und wir möchten engere Toleranzen bei der Optimierung der Log-Likelihood-Funktion verwenden. Um dies zu tun, definieren wir eine Funktion, die das Positionsargument fun akzeptiert undscipy.optimize.minimize_scalarverwendet, um fun unter den angegebenen Grenzen und Toleranzen zu minimieren>>> from scipy import optimize >>> options = {'xatol': 1e-12} # absolute tolerance on `x` >>> def optimizer(fun): ... return optimize.minimize_scalar(fun, bounds=(6, 7), ... method="bounded", options=options) >>> stats.boxcox_normmax(x, optimizer=optimizer) 6.000000000