scipy.stats.

boxcox#

scipy.stats.boxcox(x, lmbda=None, alpha=None, optimizer=None)[Quellcode]#

Gibt einen durch eine Box-Cox-Potenztransformation transformierten Datensatz zurück.

Parameter:

xndarray

Eingabearray, das transformiert werden soll.

Wenn lmbda nicht None ist, ist dies ein Alias für scipy.special.boxcox. Gibt nan zurück, wenn x < 0; gibt -inf zurück, wenn x == 0 und lmbda < 0.

Wenn lmbda None ist, muss das Array positiv, eindimensional und nicht konstant sein.

lmbdaSkalar, optional

Wenn lmbda None ist (Standardwert), wird der Wert von lmbda ermittelt, der die Log-Likelihood-Funktion maximiert, und als zweites Ausgabeargument zurückgegeben.

Wenn lmbda nicht None ist, wird die Transformation für diesen Wert durchgeführt.

alphafloat, optional

Wenn lmbda None ist und alpha nicht None ist (Standardwert), wird das 100 * (1-alpha)% Konfidenzintervall für lmbda als drittes Ausgabeargument zurückgegeben. Muss zwischen 0,0 und 1,0 liegen.

Wenn lmbda nicht None ist, wird alpha ignoriert.

optimizeraufrufbar, optional

Wenn lmbda None ist, ist optimizer der Skalar-Optimierer, der verwendet wird, um den Wert von lmbda zu finden, der die negative Log-Likelihood-Funktion minimiert. optimizer ist eine aufrufbare Funktion, die ein Argument akzeptiert

funcallable: Die Zielfunktion, die die negative Log-Likelihood-Funktion an einem gegebenen Wert von lmbda auswertet

und gibt ein Objekt zurück, z. B. eine Instanz von scipy.optimize.OptimizeResult, die den optimalen Wert von lmbda in einem Attribut x enthält.

Siehe das Beispiel in boxcox_normmax oder die Dokumentation von scipy.optimize.minimize_scalar für weitere Informationen.

Wenn lmbda nicht None ist, wird optimizer ignoriert.

Rückgabe:

boxcoxndarray: Box-Cox-potenztransformiertes Array.
maxlogfloat, optional: Wenn der Parameter lmbda None ist, ist das zweite zurückgegebene Argument das lmbda, das die Log-Likelihood-Funktion maximiert.
(min_ci, max_ci)Tuple von float, optional: Wenn der Parameter lmbda None ist und alpha nicht None ist, repräsentiert dieses Tupel aus Floats die minimale und maximale Konfidenzgrenze gegeben alpha.

Siehe auch

probplot, boxcox_normplot, boxcox_normmax, boxcox_llf

Hinweise

Die Box-Cox-Transformation ist gegeben durch

\[y = \begin{cases} \frac{x^\lambda - 1}{\lambda}, &\text{für } \lambda \neq 0 \\ \log(x), &\text{für } \lambda = 0 \end{cases}\]

boxcox erfordert, dass die Eingabedaten positiv sind. Manchmal bietet eine Box-Cox-Transformation einen Verschiebeparameter, um dies zu erreichen; boxcox tut dies nicht. Ein solcher Verschiebeparameter entspricht dem Hinzufügen einer positiven Konstanten zu x vor dem Aufruf von boxcox.

Die Konfidenzgrenzen, die zurückgegeben werden, wenn alpha angegeben ist, geben das Intervall an, in dem

\[l(\hat{\lambda}) - l(\lambda) < \frac{1}{2}\chi^2(1 - \alpha, 1),\]

wobei \(l\) die Log-Likelihood-Funktion und \(\chi^2\) die Chi-Quadrat-Funktion ist.

Referenzen

G.E.P. Box und D.R. Cox, „An Analysis of Transformations“, Journal of the Royal Statistical Society B, 26, 211-252 (1964).

Beispiele

>>> from scipy import stats
>>> import matplotlib.pyplot as plt

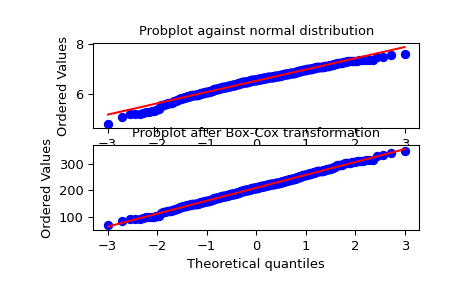
Wir generieren einige Zufallsvariaten aus einer nicht-normalen Verteilung und erstellen ein Wahrscheinlichkeitsdiagramm dafür, um zu zeigen, dass es in den Enden nicht-normal ist

>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(211)
>>> x = stats.loggamma.rvs(5, size=500) + 5
>>> prob = stats.probplot(x, dist=stats.norm, plot=ax1)
>>> ax1.set_xlabel('')
>>> ax1.set_title('Probplot against normal distribution')

Wir verwenden nun boxcox, um die Daten so zu transformieren, dass sie der Normalverteilung am nächsten kommen

>>> ax2 = fig.add_subplot(212)
>>> xt, _ = stats.boxcox(x)
>>> prob = stats.probplot(xt, dist=stats.norm, plot=ax2)
>>> ax2.set_title('Probplot after Box-Cox transformation')

>>> plt.show()