scipy.stats.

rv_histogram

class scipy.stats.rv_histogram(histogram, *args, density=None, **kwargs)

Erzeugt eine durch ein Histogramm gegebene Verteilung. Dies ist nützlich, um eine Vorlagenverteilung aus einer diskretisierten Stichprobe zu erzeugen.

Als Unterklasse der rv_continuous-Klasse erbt rv_histogram davon eine Sammlung allgemeiner Methoden (siehe rv_continuous für die vollständige Liste) und implementiert diese basierend auf den Eigenschaften der bereitgestellten diskretisierten Stichprobe.

Parameter:

histogramtuple of array_like

Tuple, das zwei Array-ähnliche Objekte enthält. Das erste enthält den Inhalt von n Bins, das zweite die (n+1) Bin-Grenzen. Insbesondere wird der Rückgabewert von numpy.histogram akzeptiert.

densitybool, optional

Wenn False, wird angenommen, dass das Histogramm proportional zu den Zählungen pro Bin ist; andernfalls wird angenommen, dass es proportional zu einer Dichte ist. Bei konstanten Bin-Breiten sind diese äquivalent, aber die Unterscheidung ist wichtig, wenn die Bin-Breiten variieren (siehe Hinweise). Wenn None (Standard), wird density=True aus Gründen der Abwärtskompatibilität gesetzt, aber es wird gewarnt, wenn die Bin-Breiten variabel sind. Setzen Sie density explizit, um die Warnung zu unterdrücken.

Hinzugefügt in Version 1.10.0.

Attribute:

random_state

Ruft den Generatorobjekt zur Erzeugung von Zufallsvariaten ab oder setzt ihn.

Methoden

__call__(*args, **kwds)	Fixiert die Verteilung für die gegebenen Argumente.
cdf(x, *args, **kwds)	Kumulative Verteilungsfunktion (CDF) der gegebenen RV.
entropy(*args, **kwds)	Differenzielle Entropie der RV.
expect([func, args, loc, scale, lb, ub, ...])	Berechnet den Erwartungswert einer Funktion bezüglich der Verteilung durch numerische Integration.
fit(data, *args, **kwds)	Gibt Schätzungen für Form (falls zutreffend), Lage und Skalenparameter aus Daten zurück.
fit_loc_scale(data, *args)	Schätzt die Parameter loc und scale aus Daten unter Verwendung des 1. und 2. Moments.
freeze(*args, **kwds)	Fixiert die Verteilung für die gegebenen Argumente.
interval(confidence, *args, **kwds)	Konfidenzintervall mit gleichen Flächen um den Median.
isf(q, *args, **kwds)	Inverse Überlebensfunktion (Inverse von sf) bei q der gegebenen RV.
logcdf(x, *args, **kwds)	Logarithmus der kumulativen Verteilungsfunktion (CDF) bei x der gegebenen RV.
logpdf(x, *args, **kwds)	Logarithmus der Wahrscheinlichkeitsdichtefunktion bei x der gegebenen RV.
logsf(x, *args, **kwds)	Logarithmus der Überlebensfunktion der gegebenen RV.
mean(*args, **kwds)	Mittelwert der Verteilung.
median(*args, **kwds)	Median der Verteilung.
moment(order, *args, **kwds)	nicht-zentrales Moment der Verteilung der angegebenen Ordnung.
nnlf(theta, x)	Negative Log-Likelihood-Funktion.
pdf(x, *args, **kwds)	Wahrscheinlichkeitsdichtefunktion (PDF) bei x der gegebenen RV.
ppf(q, *args, **kwds)	Perzentil-Punkt-Funktion (Inverse von cdf) bei q der gegebenen RV.
rvs(*args, **kwds)	Zufallsvariablen des angegebenen Typs.
sf(x, *args, **kwds)	Überlebensfunktion (1 - cdf) bei x der gegebenen RV.
stats(*args, **kwds)	Einige Statistiken der gegebenen RV.
std(*args, **kwds)	Standardabweichung der Verteilung.
support(*args, **kwargs)	Unterstützung der Verteilung.
var(*args, **kwds)	Varianz der Verteilung.

Hinweise

Wenn ein Histogramm ungleiche Bin-Breiten aufweist, gibt es einen Unterschied zwischen Histogrammen, die proportional zu den Zählungen pro Bin sind, und Histogrammen, die proportional zur Wahrscheinlichkeitsdichte über einem Bin sind. Wenn numpy.histogram mit der Standardeinstellung density=False aufgerufen wird, ist das resultierende Histogramm die Anzahl der Zählungen pro Bin, daher sollte density=False an rv_histogram übergeben werden. Wenn numpy.histogram mit density=True aufgerufen wird, ist das resultierende Histogramm in Bezug auf die Wahrscheinlichkeitsdichte, daher sollte density=True an rv_histogram übergeben werden. Um Warnungen zu vermeiden, übergeben Sie density immer explizit, wenn das Eingabe-Histogramm ungleiche Bin-Breiten aufweist.

Es gibt keine zusätzlichen Formparameter außer Lage und Skala. Die PDF wird als stückweise konstante Funktion aus dem bereitgestellten Histogramm definiert. Die CDF ist eine lineare Interpolation der PDF.

Hinzugefügt in Version 0.19.0.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Erstellt eine scipy.stats-Verteilung aus einem numpy-Histogramm

>>> import scipy.stats
>>> import numpy as np
>>> data = scipy.stats.norm.rvs(size=100000, loc=0, scale=1.5,
...                             random_state=123)
>>> hist = np.histogram(data, bins=100)
>>> hist_dist = scipy.stats.rv_histogram(hist, density=False)

Verhält sich wie eine gewöhnliche scipy rv_continuous-Verteilung

>>> hist_dist.pdf(1.0)
0.20538577847618705
>>> hist_dist.cdf(2.0)
0.90818568543056499

Die PDF ist oberhalb (unterhalb) des höchsten (niedrigsten) Bins des Histogramms Null, definiert durch das Maximum (Minimum) der ursprünglichen Stichprobe

>>> hist_dist.pdf(np.max(data))
0.0
>>> hist_dist.cdf(np.max(data))
1.0
>>> hist_dist.pdf(np.min(data))
7.7591907244498314e-05
>>> hist_dist.cdf(np.min(data))
0.0

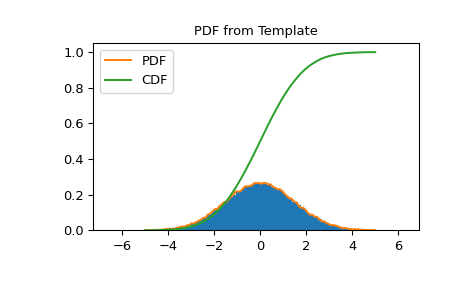
PDF und CDF folgen dem Histogramm

>>> import matplotlib.pyplot as plt
>>> X = np.linspace(-5.0, 5.0, 100)
>>> fig, ax = plt.subplots()
>>> ax.set_title("PDF from Template")
>>> ax.hist(data, density=True, bins=100)
>>> ax.plot(X, hist_dist.pdf(X), label='PDF')
>>> ax.plot(X, hist_dist.cdf(X), label='CDF')
>>> ax.legend()
>>> fig.show()

ZurückIn Tab öffnen