scipy.stats.

sobol_indices#

scipy.stats.sobol_indices(*, func, n, dists=None, method='saltelli_2010', rng=None)[Quellcode]#

Globale Sensitivitätsindizes von Sobol’.

Parameter:

funccallable oder dict(str, array_like)

Wenn func ein Callable ist, die Funktion zur Berechnung der Sobol’-Indizes. Ihre Signatur muss sein

func(x: ArrayLike) -> ArrayLike

mit x der Form (d, n) und Ausgabe der Form (s, n), wobei

d die Eingabedimension von func ist (Anzahl der Eingabevariablen),
s die Ausgabedimension von func ist (Anzahl der Ausgabevariablen) und
n die Anzahl der Stichproben ist (siehe n unten).

Die Funktionsauswertungswerte müssen endlich sein.

Wenn func ein Dictionary ist, enthält es die Funktionsauswertungen aus drei verschiedenen Arrays. Die Schlüssel müssen sein: f_A, f_B und f_AB. f_A und f_B sollten die Form (s, n) haben und f_AB sollte die Form (d, s, n) haben. Dies ist ein erweitertes Feature und Missbrauch kann zu falschen Analysen führen.

nint

Anzahl der Stichproben, die zur Erzeugung der Matrizen A und B verwendet werden. Muss eine Zweierpotenz sein. Die Gesamtzahl der Punkte, an denen func ausgewertet wird, beträgt n*(d+2).

distslist(distributions), optional

Liste der Verteilung jedes Parameters. Die Verteilung der Parameter hängt von der Anwendung ab und sollte sorgfältig gewählt werden. Es wird angenommen, dass die Parameter unabhängig verteilt sind, was bedeutet, dass es keine Einschränkung oder Beziehung zwischen ihren Werten gibt.

Distributionen müssen Instanzen einer Klasse mit einer ppf-Methode sein.

Muss angegeben werden, wenn func ein Callable ist, andernfalls wird es ignoriert.

methodCallable oder str, Standard: ‘saltelli_2010’

Methode zur Berechnung der ersten und gesamten Sobol’-Indizes.

Wenn ein Callable, muss seine Signatur lauten:

func(f_A: np.ndarray, f_B: np.ndarray, f_AB: np.ndarray)
-> Tuple[np.ndarray, np.ndarray]

mit f_A, f_B der Form (s, n) und f_AB der Form (d, s, n). Diese Arrays enthalten die Funktionsauswertungen aus drei verschiedenen Stichprobensätzen. Die Ausgabe ist ein Tupel der ersten und gesamten Indizes mit der Form (s, d). Dies ist ein erweitertes Feature und Missbrauch kann zu falschen Analysen führen.

rngnumpy.random.Generator, optional

Zustand des Pseudozufallszahlengenerators. Wenn rng None ist, wird ein neuer numpy.random.Generator mit Entropie vom Betriebssystem erstellt. Typen außer numpy.random.Generator werden an numpy.random.default_rng übergeben, um einen Generator zu instanziieren.

Geändert in Version 1.15.0: Als Teil des SPEC-007-Übergangs von der Verwendung von numpy.random.RandomState zu numpy.random.Generator wurde dieses Schlüsselwort von random_state in rng geändert. Für eine Übergangszeit werden beide Schlüsselwörter weiterhin funktionieren, obwohl nur eines gleichzeitig angegeben werden darf. Nach der Übergangszeit werden Funktionsaufrufe mit dem Schlüsselwort random_state Warnungen ausgeben. Nach einer Deprezierungsperiode wird das Schlüsselwort random_state entfernt.

Rückgabe:

resSobolResult

Ein Objekt mit den Attributen

first_orderndarray von Form (s, d): Erste Ordnung Sobol’-Indizes.
total_orderndarray von Form (s, d): Gesamtordnung Sobol’-Indizes.

Und Methode

bootstrap(confidence_level: float, n_resamples: int) -> BootstrapSobolResult

Eine Methode, die Konfidenzintervalle für die Indizes liefert. Weitere Details finden Sie unter scipy.stats.bootstrap.

Das Bootstrapping erfolgt sowohl für die Indizes erster Ordnung als auch für die Gesamtindizes, und sie sind in BootstrapSobolResult unter den Attributen first_order und total_order verfügbar.

Hinweise

Die Sobol’-Methode [1], [2] ist eine varianzbasierte Sensitivitätsanalyse, die den Beitrag jedes Parameters zur Varianz der interessierenden Größen (QoIs; d. h. der Ausgaben von func) ermittelt. Entsprechende Beiträge können zur Rangordnung der Parameter und zur Einschätzung der Modellkomplexität durch Berechnung der effektiven (oder mittleren) Dimension des Modells verwendet werden.

Hinweis

Parameter werden als unabhängig verteilt angenommen. Jeder Parameter kann dennoch jeder Verteilung folgen. Tatsächlich ist die Verteilung sehr wichtig und sollte der realen Verteilung der Parameter entsprechen.

Sie verwendet eine funktionale Zerlegung der Varianz der Funktion zur Untersuchung

\[\mathbb{V}(Y) = \sum_{i}^{d} \mathbb{V}_i (Y) + \sum_{i<j}^{d} \mathbb{V}_{ij}(Y) + ... + \mathbb{V}_{1,2,...,d}(Y),\]

führt bedingte Varianzen ein

\[\mathbb{V}_i(Y) = \mathbb{V}[\mathbb{E}(Y|x_i)] \qquad \mathbb{V}_{ij}(Y) = \mathbb{V}[\mathbb{E}(Y|x_i x_j)] - \mathbb{V}_i(Y) - \mathbb{V}_j(Y),\]

Sobol’-Indizes werden ausgedrückt als

\[S_i = \frac{\mathbb{V}_i(Y)}{\mathbb{V}[Y]} \qquad S_{ij} =\frac{\mathbb{V}_{ij}(Y)}{\mathbb{V}[Y]}.\]

\(S_{i}\) entspricht dem Term erster Ordnung, der den Beitrag des i-ten Parameters bewertet, während \(S_{ij}\) dem Term zweiter Ordnung entspricht, der über den Beitrag von Wechselwirkungen zwischen dem i-ten und dem j-ten Parameter informiert. Diese Gleichungen können verallgemeinert werden, um Terme höherer Ordnung zu berechnen. Diese sind jedoch teuer zu berechnen und ihre Interpretation ist komplex. Deshalb werden nur Indizes erster Ordnung bereitgestellt.

Gesamtordnung-Indizes repräsentieren den globalen Beitrag der Parameter zur Varianz der QoI und sind definiert als

\[S_{T_i} = S_i + \sum_j S_{ij} + \sum_{j,k} S_{ijk} + ... = 1 - \frac{\mathbb{V}[\mathbb{E}(Y|x_{\sim i})]}{\mathbb{V}[Y]}.\]

Die Summe der Indizes erster Ordnung ist höchstens 1, während die Summe der Gesamtordnung-Indizes mindestens 1 beträgt. Wenn keine Wechselwirkungen vorhanden sind, sind die Indizes erster und Gesamtordnung gleich, und sowohl die Indizes erster als auch Gesamtordnung summieren sich zu 1.

Warnung

Negative Sobol’-Werte sind auf numerische Fehler zurückzuführen. Eine Erhöhung der Anzahl der Punkte n sollte helfen.

Die Anzahl der für eine gute Analyse erforderlichen Stichproben steigt mit der Dimensionalität des Problems. Z. B. für ein 3-dimensionales Problem sollten mindestens n >= 2**12 betrachtet werden. Je komplexer das Modell ist, desto mehr Stichproben werden benötigt.

Selbst für ein rein additives Modell summieren sich die Indizes aufgrund von Rauschen möglicherweise nicht zu 1.

Referenzen

[1]

Sobol, I. M.. „Sensitivity analysis for nonlinear mathematical models.“ Mathematical Modeling and Computational Experiment, 1:407-414, 1993.

[2]

Sobol, I. M. (2001). „Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates.“ Mathematics and Computers in Simulation, 55(1-3):271-280, DOI:10.1016/S0378-4754(00)00270-6, 2001.

[3]

Saltelli, A. „Making best use of model evaluations to compute sensitivity indices.“ Computer Physics Communications, 145(2):280-297, DOI:10.1016/S0010-4655(02)00280-1, 2002.

[4]

Saltelli, A., M. Ratto, T. Andres, F. Campolongo, J. Cariboni, D. Gatelli, M. Saisana und S. Tarantola. „Global Sensitivity Analysis. The Primer.“ 2007.

[5]

Saltelli, A., P. Annoni, I. Azzini, F. Campolongo, M. Ratto und S. Tarantola. „Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index.“ Computer Physics Communications, 181(2):259-270, DOI:10.1016/j.cpc.2009.09.018, 2010.

[6]

Ishigami, T. und T. Homma. „An importance quantification technique in uncertainty analysis for computer models.“ IEEE, DOI:10.1109/ISUMA.1990.151285, 1990.

Beispiele

Das Folgende ist ein Beispiel mit der Ishigami-Funktion [6]

\[Y(\mathbf{x}) = \sin x_1 + 7 \sin^2 x_2 + 0.1 x_3^4 \sin x_1,\]

mit \(\mathbf{x} \in [-\pi, \pi]^3\). Diese Funktion weist eine starke Nichtlinearität und Nichtmonotonie auf.

Denken Sie daran, dass Sobol’-Indizes davon ausgehen, dass Stichproben unabhängig verteilt sind. In diesem Fall verwenden wir eine gleichmäßige Verteilung auf jedem Marginal.

>>> import numpy as np
>>> from scipy.stats import sobol_indices, uniform
>>> rng = np.random.default_rng()
>>> def f_ishigami(x):
...     f_eval = (
...         np.sin(x[0])
...         + 7 * np.sin(x[1])**2
...         + 0.1 * (x[2]**4) * np.sin(x[0])
...     )
...     return f_eval
>>> indices = sobol_indices(
...     func=f_ishigami, n=1024,
...     dists=[
...         uniform(loc=-np.pi, scale=2*np.pi),
...         uniform(loc=-np.pi, scale=2*np.pi),
...         uniform(loc=-np.pi, scale=2*np.pi)
...     ],
...     rng=rng
... )
>>> indices.first_order
array([0.31637954, 0.43781162, 0.00318825])
>>> indices.total_order
array([0.56122127, 0.44287857, 0.24229595])

Konfidenzintervalle können durch Bootstrapping erhalten werden.

>>> boot = indices.bootstrap()

Anschließend können diese Informationen einfach visualisiert werden.

>>> import matplotlib.pyplot as plt
>>> fig, axs = plt.subplots(1, 2, figsize=(9, 4))
>>> _ = axs[0].errorbar(
...     [1, 2, 3], indices.first_order, fmt='o',
...     yerr=[
...         indices.first_order - boot.first_order.confidence_interval.low,
...         boot.first_order.confidence_interval.high - indices.first_order
...     ],
... )
>>> axs[0].set_ylabel("First order Sobol' indices")
>>> axs[0].set_xlabel('Input parameters')
>>> axs[0].set_xticks([1, 2, 3])
>>> _ = axs[1].errorbar(
...     [1, 2, 3], indices.total_order, fmt='o',
...     yerr=[
...         indices.total_order - boot.total_order.confidence_interval.low,
...         boot.total_order.confidence_interval.high - indices.total_order
...     ],
... )
>>> axs[1].set_ylabel("Total order Sobol' indices")
>>> axs[1].set_xlabel('Input parameters')
>>> axs[1].set_xticks([1, 2, 3])
>>> plt.tight_layout()
>>> plt.show()

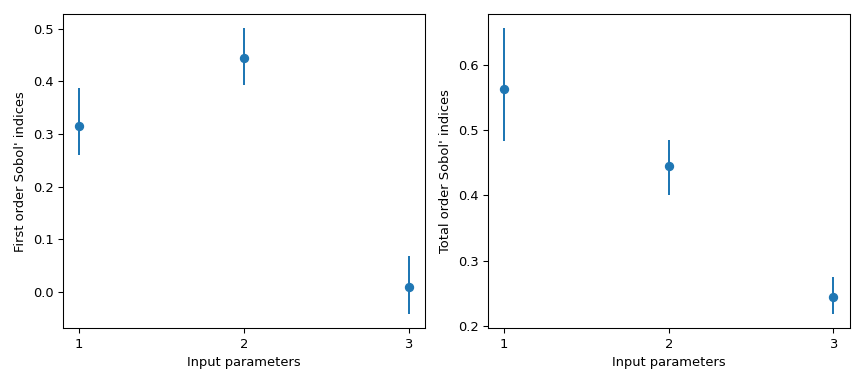
../../_images/scipy-stats-sobol_indices-1_00_00.png

Hinweis

Standardmäßig hat scipy.stats.uniform den Träger [0, 1]. Mit den Parametern loc und scale erhält man die gleichmäßige Verteilung auf [loc, loc + scale].

Dieses Ergebnis ist besonders interessant, da der Index erster Ordnung \(S_{x_3} = 0\) ist, während seine Gesamtordnung \(S_{T_{x_3}} = 0.244\) beträgt. Dies bedeutet, dass Wechselwirkungen höherer Ordnung mit \(x_3\) für die Differenz verantwortlich sind. Fast 25% der beobachteten Varianz der QoI sind auf die Korrelationen zwischen \(x_3\) und \(x_1\) zurückzuführen, obwohl \(x_3\) allein keinen Einfluss auf die QoI hat.

Das Folgende gibt eine visuelle Erklärung der Sobol’-Indizes für diese Funktion. Generieren wir 1024 Stichproben in \([-\pi, \pi]^3\) und berechnen den Wert der Ausgabe.

>>> from scipy.stats import qmc
>>> n_dim = 3
>>> p_labels = ['$x_1$', '$x_2$', '$x_3$']
>>> sample = qmc.Sobol(d=n_dim, seed=rng).random(1024)
>>> sample = qmc.scale(
...     sample=sample,
...     l_bounds=[-np.pi, -np.pi, -np.pi],
...     u_bounds=[np.pi, np.pi, np.pi]
... )
>>> output = f_ishigami(sample.T)

Jetzt können wir Streudiagramme der Ausgabe in Bezug auf jeden Parameter erstellen. Dies ist eine visuelle Methode, um zu verstehen, wie jeder Parameter die Ausgabe der Funktion beeinflusst.

>>> fig, ax = plt.subplots(1, n_dim, figsize=(12, 4))
>>> for i in range(n_dim):
...     xi = sample[:, i]
...     ax[i].scatter(xi, output, marker='+')
...     ax[i].set_xlabel(p_labels[i])
>>> ax[0].set_ylabel('Y')
>>> plt.tight_layout()
>>> plt.show()

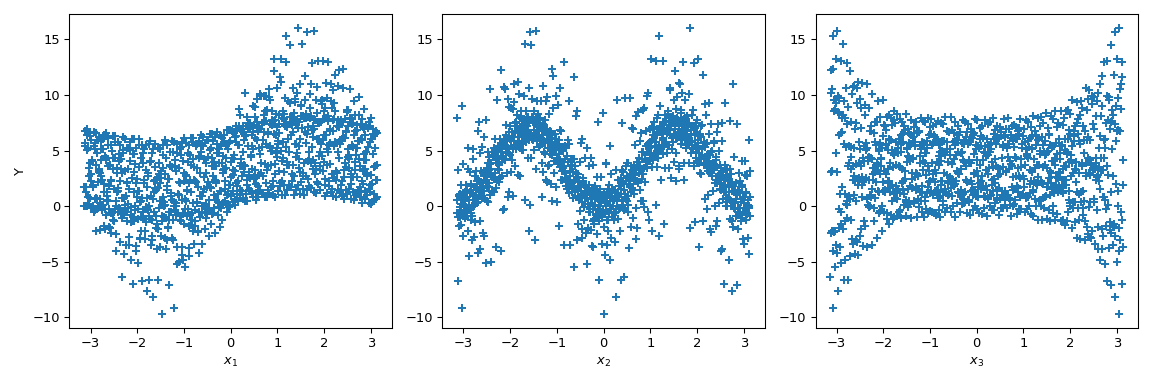
../../_images/scipy-stats-sobol_indices-1_01_00.png

Nun geht Sobol’ einen Schritt weiter: Durch Konditionierung des Ausgabewerts auf gegebene Parameterwerte (schwarze Linien) wird der bedingte Ausgabemittelwert berechnet. Er entspricht dem Term \(\mathbb{E}(Y|x_i)\). Die Varianz dieses Terms ergibt den Zähler der Sobol’-Indizes.

>>> mini = np.min(output)
>>> maxi = np.max(output)
>>> n_bins = 10
>>> bins = np.linspace(-np.pi, np.pi, num=n_bins, endpoint=False)
>>> dx = bins[1] - bins[0]
>>> fig, ax = plt.subplots(1, n_dim, figsize=(12, 4))
>>> for i in range(n_dim):
...     xi = sample[:, i]
...     ax[i].scatter(xi, output, marker='+')
...     ax[i].set_xlabel(p_labels[i])
...     for bin_ in bins:
...         idx = np.where((bin_ <= xi) & (xi <= bin_ + dx))
...         xi_ = xi[idx]
...         y_ = output[idx]
...         ave_y_ = np.mean(y_)
...         ax[i].plot([bin_ + dx/2] * 2, [mini, maxi], c='k')
...         ax[i].scatter(bin_ + dx/2, ave_y_, c='r')
>>> ax[0].set_ylabel('Y')
>>> plt.tight_layout()
>>> plt.show()

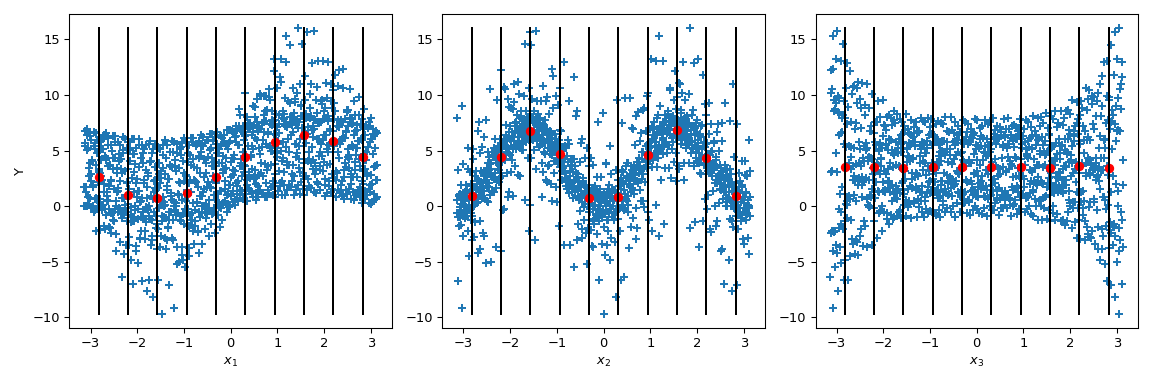
../../_images/scipy-stats-sobol_indices-1_02_00.png

Wenn wir uns \(x_3\) ansehen, ist die Varianz des Mittelwerts null, was zu \(S_{x_3} = 0\) führt. Aber wir können weiter beobachten, dass die Varianz der Ausgabe entlang der Parameterwerte von \(x_3\) nicht konstant ist. Diese Heteroskedastizität wird durch Wechselwirkungen höherer Ordnung erklärt. Darüber hinaus ist eine Heteroskedastizität auch bei \(x_1\) bemerkbar, was zu einer Wechselwirkung zwischen \(x_3\) und \(x_1\) führt. Bei \(x_2\) scheint die Varianz konstant zu sein, und daher kann keine Wechselwirkung mit diesem Parameter angenommen werden.

Dieser Fall ist visuell relativ einfach zu analysieren – obwohl es sich nur um eine qualitative Analyse handelt. Wenn jedoch die Anzahl der Eingabeparameter zunimmt, wird eine solche Analyse unrealistisch, da es schwierig wäre, Schlussfolgerungen über Terme höherer Ordnung zu ziehen. Daher der Nutzen der Verwendung von Sobol’-Indizes.