scipy.stats.

ppcc_max

scipy.stats.ppcc_max(x, brack=(0.0, 1.0), dist='tukeylambda')

Berechnet den Shape-Parameter, der den PPCC maximiert.

Das Probability Plot Correlation Coefficient (PPCC) Diagramm kann verwendet werden, um den optimalen Shape-Parameter für eine eindimensionale Verteilungsfamilie zu bestimmen. ppcc_max gibt den Shape-Parameter zurück, der den Probability Plot Correlation Coefficient für die gegebenen Daten für eine eindimensionale Verteilungsfamilie maximieren würde.

Parameter:

xarray_like

Eingabearray.

bracktuple, optional

Tripel (a,b,c) wobei (a<b<c). Wenn das Intervall aus zwei Zahlen (a, c) besteht, werden diese als Startintervall für eine absteigende Intervallsuche angenommen (siehe scipy.optimize.brent).

diststr oder stats.distributions-Instanz, optional

Name der Verteilung oder Verteilungsfunktion. Objekte, die ausreichend wie eine stats.distributions-Instanz aussehen (d.h. sie haben eine ppf Methode), werden ebenfalls akzeptiert. Der Standardwert ist 'tukeylambda'.

Rückgabe:

shape_valuefloat

Der Shape-Parameter, bei dem der Probability Plot Correlation Coefficient seinen Maximalwert erreicht.

Siehe auch

ppcc_plot, probplot, boxcox

Hinweise

Das Schlüsselwort `brack` dient als Ausgangspunkt, was in Randfällen nützlich ist. Man kann ein Diagramm verwenden, um eine grobe visuelle Schätzung der Position des Maximums zu erhalten und die Suche dort in der Nähe zu starten.

Referenzen

[1]

J.J. Filliben, „The Probability Plot Correlation Coefficient Test for Normality“, Technometrics, Vol. 17, S. 111-117, 1975.

[2]

Engineering Statistics Handbook, NIST/SEMATEC, https://www.itl.nist.gov/div898/handbook/eda/section3/ppccplot.htm

Beispiele

Probieren Sie es in Ihrem Browser aus!

Zuerst generieren wir einige Zufallsdaten aus einer Weibull-Verteilung mit dem Shape-Parameter 2.5

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> c = 2.5
>>> x = stats.weibull_min.rvs(c, scale=4, size=2000, random_state=rng)

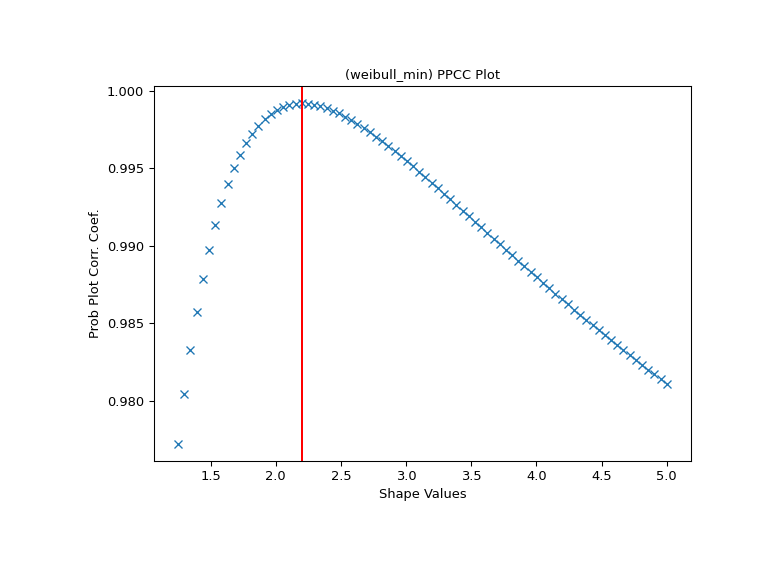
Generieren Sie das PPCC-Diagramm für diese Daten mit der Weibull-Verteilung.

>>> fig, ax = plt.subplots(figsize=(8, 6))
>>> res = stats.ppcc_plot(x, c/2, 2*c, dist='weibull_min', plot=ax)

Wir berechnen den Wert, bei dem der Shape-Parameter sein Maximum erreichen sollte, und zeichnen dort eine rote Linie. Die Linie sollte mit dem höchsten Punkt im PPCC-Diagramm übereinstimmen.

>>> cmax = stats.ppcc_max(x, brack=(c/2, 2*c), dist='weibull_min')
>>> ax.axvline(cmax, color='r')
>>> plt.show()

ZurückIn Tab öffnen