scipy.stats.

tukey_hsd#

scipy.stats.tukey_hsd(*args, equal_var=True)[Quellcode]#

Führt den Tukey-HSD-Test auf Gleichheit der Mittelwerte über mehrere Behandlungen durch.

Der Tukey-HSD-Test (Honestly Significant Difference) führt paarweise Vergleiche der Mittelwerte einer Stichprobensammlung durch. Während die ANOVA (z. B. f_oneway) prüft, ob die wahren Mittelwerte, die jeder Stichprobe zugrunde liegen, identisch sind, ist Tukey's HSD ein Post-hoc-Test, der verwendet wird, um den Mittelwert jeder Stichprobe mit dem Mittelwert jeder anderen Stichprobe zu vergleichen.

Die Nullhypothese besagt, dass die Verteilungen, die den Stichproben zugrunde liegen, alle den gleichen Mittelwert haben. Die Teststatistik, die für jede mögliche Paarung von Stichproben berechnet wird, ist einfach die Differenz zwischen den Stichprobenmittelwerten. Für jedes Paar ist der p-Wert die Wahrscheinlichkeit unter der Nullhypothese (und anderen Annahmen; siehe Hinweise), ein derart extremes Ergebnis der Statistik zu beobachten, wenn man bedenkt, dass viele paarweise Vergleiche durchgeführt werden. Konfidenzintervalle für die Differenz zwischen jedem Paar von Mittelwerten sind ebenfalls verfügbar.

Parameter:

stichprobe1, stichprobe2, …array_like: Die Stichprobenmessungen für jede Gruppe. Es müssen mindestens zwei Argumente vorhanden sein.
equal_var: bool, optional: Wenn True (Standard) und gleiche Stichprobengröße, wird der Tukey-HSD-Test [6] durchgeführt. Wenn True und ungleiche Stichprobengröße, wird der Tukey-Kramer-Test [4] durchgeführt. Wenn False, wird der Games-Howell-Test [7] durchgeführt, der keine gleichen Varianzen annimmt.

Rückgabe:

resultTukeyHSDResult Instanz

Der Rückgabewert ist ein Objekt mit folgenden Attributen:

statisticfloat ndarray: Die berechnete Statistik des Tests für jeden Vergleich. Das Element an Index (i, j) ist die Statistik für den Vergleich zwischen den Gruppen i und j.
pvaluefloat ndarray: Der berechnete p-Wert des Tests für jeden Vergleich. Das Element an Index (i, j) ist der p-Wert für den Vergleich zwischen den Gruppen i und j.

Das Objekt hat die folgenden Methoden

confidence_interval(confidence_level=0.95): Berechnet das Konfidenzintervall für das angegebene Konfidenzniveau.

Siehe auch

dunnett: führt einen Vergleich der Mittelwerte gegen eine Kontrollgruppe durch.

Hinweise

Die Verwendung dieses Tests beruht auf mehreren Annahmen.

Die Beobachtungen sind innerhalb und zwischen den Gruppen unabhängig.
Die Beobachtungen innerhalb jeder Gruppe sind normalverteilt.
Die Verteilungen, aus denen die Stichproben gezogen werden, haben die gleiche endliche Varianz.

Die ursprüngliche Formulierung des Tests galt für Stichproben gleicher Größe, die aus Populationen mit angenommenen gleichen Varianzen gezogen wurden [6]. Bei ungleichen Stichprobengrößen verwendet der Test die Tukey-Kramer-Methode [4]. Wenn gleiche Varianzen nicht angenommen werden (equal_var=False), verwendet der Test die Games-Howell-Methode [7].

Referenzen

[1]

NIST/SEMATECH e-Handbuch für statistische Methoden, „7.4.7.1. Tuckeys Methode.“ https://www.itl.nist.gov/div898/handbook/prc/section4/prc471.htm, 28. November 2020.

[2]

Abdi, Herve & Williams, Lynne. (2021). „Tukey’s Honestly Significant Difference (HSD) Test.“ https://personal.utdallas.edu/~herve/abdi-HSD2010-pretty.pdf

[3]

„One-Way ANOVA Using SAS PROC ANOVA & PROC GLM.“ SAS Tutorials, 2007, www.stattutorials.com/SAS/TUTORIAL-PROC-GLM.htm.

[4] (1,2)

Kramer, Clyde Young. „Extension of Multiple Range Tests to Group Means with Unequal Numbers of Replications.“ Biometrics, vol. 12, no. 3, 1956, pp. 307-310. JSTOR, www.jstor.org/stable/3001469. Aufgerufen am 25. Mai 2021.

[5]

NIST/SEMATECH e-Handbuch für statistische Methoden, „7.4.3.3. Die ANOVA-Tabelle und Hypothesentests zu Mittelwerten“ https://www.itl.nist.gov/div898/handbook/prc/section4/prc433.htm, 2. Juni 2021.

[6]

Tukey, John W. „Comparing Individual Means in the Analysis of Variance.“ Biometrics, vol. 5, no. 2, 1949, pp. 99-114. JSTOR, www.jstor.org/stable/3001913. Aufgerufen am 14. Juni 2021.

[7] (1,2)

P. A. Games und J. F. Howell, „Pairwise Multiple Comparison Procedures with Unequal N’s and/or Variances: A Monte Carlo Study,“ Journal of Educational Statistics, vol. 1, no. 2, pp. 113-125, Juni 1976, doi: https://doi.org/10.3102/10769986001002113.

Beispiele

Hier sind einige Daten, die die Zeit bis zur Linderung von drei Marken von Kopfschmerzmitteln vergleichen, gemessen in Minuten. Daten angepasst aus [3].

>>> import numpy as np
>>> from scipy.stats import tukey_hsd
>>> group0 = [24.5, 23.5, 26.4, 27.1, 29.9]
>>> group1 = [28.4, 34.2, 29.5, 32.2, 30.1]
>>> group2 = [26.1, 28.3, 24.3, 26.2, 27.8]

Wir möchten sehen, ob es signifikante Unterschiede zwischen den Mitteln der Gruppen gibt. Betrachten Sie zuerst ein Box-Whisker-Diagramm.

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)
>>> ax.boxplot([group0, group1, group2])
>>> ax.set_xticklabels(["group0", "group1", "group2"]) 
>>> ax.set_ylabel("mean") 
>>> plt.show()

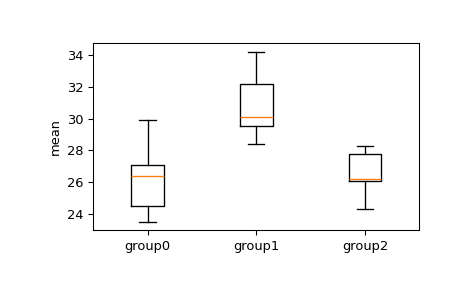
../../_images/scipy-stats-tukey_hsd-1_00_00.png

Aus dem Box-Whisker-Diagramm können wir eine Überlappung der Interquartilsbereiche zwischen Gruppe 1 und Gruppe 2 sowie Gruppe 3 erkennen. Wir können jedoch den tukey_hsd-Test anwenden, um festzustellen, ob der Unterschied zwischen den Mittelwerten signifikant ist. Wir legen ein Signifikanzniveau von 0,05 fest, um die Nullhypothese zu verwerfen.

>>> res = tukey_hsd(group0, group1, group2)
>>> print(res)
Pairwise Group Comparisons (95.0% Confidence Interval)
Comparison  Statistic  p-value  Lower CI  Upper CI
 (0 - 1)     -4.600     0.014    -8.249    -0.951
 (0 - 2)     -0.260     0.980    -3.909     3.389
 (1 - 0)      4.600     0.014     0.951     8.249
 (1 - 2)      4.340     0.020     0.691     7.989
 (2 - 0)      0.260     0.980    -3.389     3.909
 (2 - 1)     -4.340     0.020    -7.989    -0.691

Die Nullhypothese besagt, dass jede Gruppe denselben Mittelwert hat. Der p-Wert für Vergleiche zwischen group0 und group1 sowie group1 und group2 überschreitet 0,05 nicht, daher verwerfen wir die Nullhypothese, dass sie die gleichen Mittelwerte haben. Der p-Wert des Vergleichs zwischen group0 und group2 überschreitet 0,05, daher akzeptieren wir die Nullhypothese, dass es keinen signifikanten Unterschied zwischen ihren Mittelwerten gibt.

Wir können auch das Konfidenzintervall für unser gewähltes Konfidenzniveau berechnen.

>>> group0 = [24.5, 23.5, 26.4, 27.1, 29.9]
>>> group1 = [28.4, 34.2, 29.5, 32.2, 30.1]
>>> group2 = [26.1, 28.3, 24.3, 26.2, 27.8]
>>> result = tukey_hsd(group0, group1, group2)
>>> conf = res.confidence_interval(confidence_level=.99)
>>> for ((i, j), l) in np.ndenumerate(conf.low):
...     # filter out self comparisons
...     if i != j:
...         h = conf.high[i,j]
...         print(f"({i} - {j}) {l:>6.3f} {h:>6.3f}")
(0 - 1) -9.480  0.280
(0 - 2) -5.140  4.620
(1 - 0) -0.280  9.480
(1 - 2) -0.540  9.220
(2 - 0) -4.620  5.140
(2 - 1) -9.220  0.540