scipy.stats.vonmises_line

scipy.stats.vonmises_line = <scipy.stats._continuous_distns.vonmises_gen object>

Eine Von Mises-kontinuierliche Zufallsvariable.

Als Instanz der Klasse rv_continuous erbt das Objekt vonmises_line von ihr eine Sammlung generischer Methoden (siehe unten für die vollständige Liste) und vervollständigt diese mit Details, die für diese spezielle Verteilung spezifisch sind.

Methoden

rvs(kappa, loc=0, scale=1, size=1, random_state=None)	Zufallsvariaten.
pdf(x, kappa, loc=0, scale=1)	Wahrscheinlichkeitsdichtefunktion.
logpdf(x, kappa, loc=0, scale=1)	Logarithmus der Wahrscheinlichkeitsdichtefunktion.
cdf(x, kappa, loc=0, scale=1)	Kumulative Verteilungsfunktion.
logcdf(x, kappa, loc=0, scale=1)	Logarithmus der kumulativen Verteilungsfunktion.
sf(x, kappa, loc=0, scale=1)	Überlebensfunktion (auch definiert als 1 - cdf, aber sf ist manchmal genauer).
logsf(x, kappa, loc=0, scale=1)	Logarithmus der Überlebensfunktion.
ppf(q, kappa, loc=0, scale=1)	Perzentilpunktfunktion (Umkehrung von cdf — Perzentile).
isf(q, kappa, loc=0, scale=1)	Umgekehrte Überlebensfunktion (Umkehrung von sf).
moment(order, kappa, loc=0, scale=1)	Nichtzentrales Moment der angegebenen Ordnung.
stats(kappa, loc=0, scale=1, moments=’mv’)	Mittelwert(‚m‘), Varianz(‚v‘), Schiefe(‚s‘) und/oder Kurtosis(‚k‘).
entropy(kappa, loc=0, scale=1)	(Differential-)Entropie der RV.
fit(data)	Parameterschätzungen für generische Daten. Siehe scipy.stats.rv_continuous.fit für eine detaillierte Dokumentation der Schlüsselwortargumente.
expect(func, args=(kappa,), loc=0, scale=1, lb=None, ub=None, conditional=False, **kwds)	Erwartungswert einer Funktion (einer Variablen) bezüglich der Verteilung.
median(kappa, loc=0, scale=1)	Median der Verteilung.
mean(kappa, loc=0, scale=1)	Mittelwert der Verteilung.
var(kappa, loc=0, scale=1)	Varianz der Verteilung.
std(kappa, loc=0, scale=1)	Standardabweichung der Verteilung.
interval(confidence, kappa, loc=0, scale=1)	Konfidenzintervall mit gleichen Flächen um den Median.

Siehe auch

scipy.stats.vonmises_fisher

Von-Mises Fisher-Verteilung auf einer Hypersphäre

Hinweise

Die Wahrscheinlichkeitsdichtefunktion für vonmises und vonmises_line ist

\[f(x, \kappa) = \frac{ \exp(\kappa \cos(x)) }{ 2 \pi I_0(\kappa) }\]

für \(-\pi \le x \le \pi\), \(\kappa \ge 0\). \(I_0\) ist die modifizierte Besselfunktion der Ordnung Null (scipy.special.i0).

vonmises ist eine zirkuläre Verteilung, die die Verteilung nicht auf ein festes Intervall beschränkt. Derzeit gibt es kein zirkuläres Verteilungsframework in SciPy. Die cdf ist so implementiert, dass cdf(x + 2*np.pi) == cdf(x) + 1 gilt.

vonmises_line ist die gleiche Verteilung, definiert auf \([-\pi, \pi]\) auf der reellen Achse. Dies ist eine reguläre (d.h. nicht-zirkuläre) Verteilung.

Hinweis zu Verteilungsparametern: vonmises und vonmises_line nehmen kappa als Formparameter (Konzentration) und loc als Ort (zirkulärer Mittelwert). Ein scale-Parameter wird akzeptiert, hat aber keine Auswirkung.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Importieren Sie die notwendigen Module.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.stats import vonmises

Definiere Verteilungsparameter.

>>> loc = 0.5 * np.pi  # circular mean
>>> kappa = 1  # concentration

Berechne die Wahrscheinlichkeitsdichte bei x=0 über die Methode pdf.

>>> vonmises.pdf(0, loc=loc, kappa=kappa)
0.12570826359722018

Überprüfe, ob die Perzentilfunktion ppf die kumulative Verteilungsfunktion cdf bis auf Gleitkomma-Genauigkeit umkehrt.

>>> x = 1
>>> cdf_value = vonmises.cdf(x, loc=loc, kappa=kappa)
>>> ppf_value = vonmises.ppf(cdf_value, loc=loc, kappa=kappa)
>>> x, cdf_value, ppf_value
(1, 0.31489339900904967, 1.0000000000000004)

Ziehe 1000 Zufallsvariaten durch Aufruf der Methode rvs.

>>> sample_size = 1000
>>> sample = vonmises(loc=loc, kappa=kappa).rvs(sample_size)

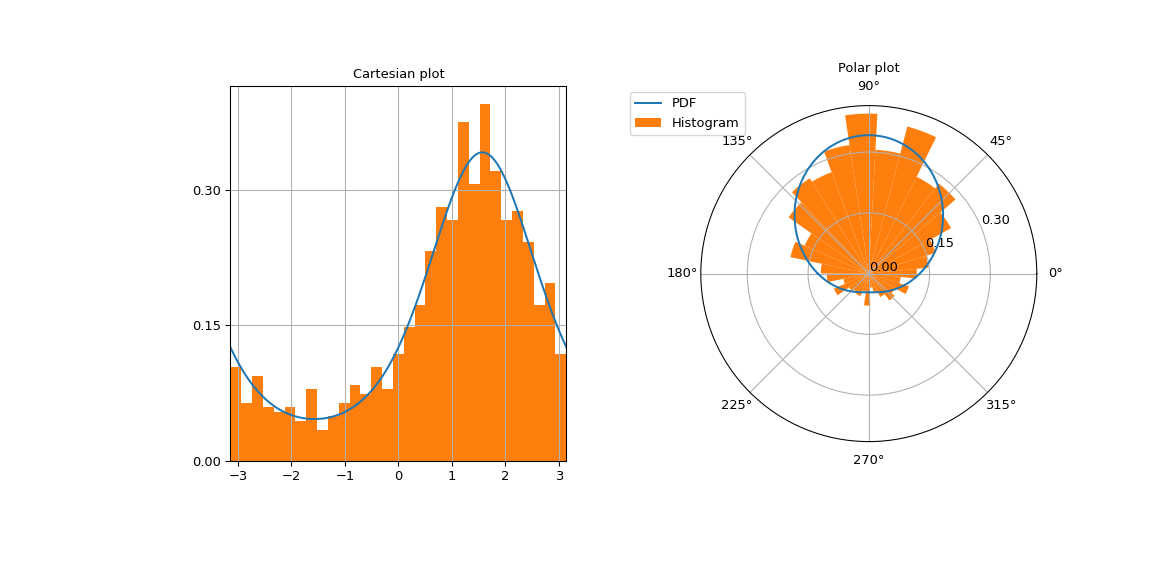
Plotte die von-Mises-Dichte auf einem kartesischen und einem Polargitter, um zu betonen, dass es sich um eine zirkuläre Verteilung handelt.

>>> fig = plt.figure(figsize=(12, 6))
>>> left = plt.subplot(121)
>>> right = plt.subplot(122, projection='polar')
>>> x = np.linspace(-np.pi, np.pi, 500)
>>> vonmises_pdf = vonmises.pdf(x, loc=loc, kappa=kappa)
>>> ticks = [0, 0.15, 0.3]

Das linke Bild enthält die kartesische Darstellung.

>>> left.plot(x, vonmises_pdf)
>>> left.set_yticks(ticks)
>>> number_of_bins = int(np.sqrt(sample_size))
>>> left.hist(sample, density=True, bins=number_of_bins)
>>> left.set_title("Cartesian plot")
>>> left.set_xlim(-np.pi, np.pi)
>>> left.grid(True)

Das rechte Bild enthält die Polardarstellung.

>>> right.plot(x, vonmises_pdf, label="PDF")
>>> right.set_yticks(ticks)
>>> right.hist(sample, density=True, bins=number_of_bins,
...            label="Histogram")
>>> right.set_title("Polar plot")
>>> right.legend(bbox_to_anchor=(0.15, 1.06))

ZurückIn Tab öffnen