scipy.integrate.

cumulative_simpson#

scipy.integrate.cumulative_simpson(y, *, x=None, dx=1.0, axis=-1, initial=None)[Quelle]#

Integrieren Sie y(x) kumulativ mit der zusammengesetzten Simpson'schen 1/3-Regel. Das Integral der Abtastwerte an jedem Punkt wird berechnet, indem eine quadratische Beziehung zwischen jedem Punkt und den beiden benachbarten Punkten angenommen wird.

Parameter:

yarray_like: Zu integrierende Werte. Benötigt mindestens einen Punkt entlang der axis. Wenn zwei oder weniger Punkte entlang der axis bereitgestellt werden, ist die Simpson'sche Integration nicht möglich und das Ergebnis wird mit cumulative_trapezoid berechnet.
xarray_like, optional: Die zu integrierende Koordinate. Muss die gleiche Form wie y haben oder 1D mit der gleichen Länge wie y entlang der axis sein. x muss ebenfalls streng monoton steigend entlang der axis sein. Wenn x None (Standard) ist, erfolgt die Integration unter Verwendung des Abstands dx zwischen aufeinanderfolgenden Elementen in y.
dxSkalar oder array_like, optional: Abstand zwischen den Elementen von y. Wird nur verwendet, wenn x None ist. Kann entweder ein Float oder ein Array mit der gleichen Form wie y sein, aber mit der Länge eins entlang der axis. Standard ist 1,0.
axisint, optional: Gibt die Achse an, entlang der integriert werden soll. Standard ist -1 (letzte Achse).
initialSkalar oder array_like, optional: Wenn angegeben, fügen Sie diesen Wert am Anfang des zurückgegebenen Ergebnisses ein und addieren Sie ihn zum Rest des Ergebnisses. Standard ist None, was bedeutet, dass kein Wert bei x[0] zurückgegeben wird und res entlang der Integrationsachse ein Element weniger als y hat. Kann entweder ein Float oder ein Array mit der gleichen Form wie y sein, aber mit der Länge eins entlang der axis.

Rückgabe:

resndarray: Das Ergebnis der kumulativen Integration von y entlang der axis. Wenn initial None ist, ist die Form so, dass die Integrationsachse einen Wert weniger als y hat. Wenn initial angegeben ist, ist die Form gleich der von y.

Siehe auch

numpy.cumsum
cumulative_trapezoid: kumulative Integration mit der zusammengesetzten Trapezregel
simpson: Integrator für abgetastete Daten unter Verwendung der zusammengesetzten Simpson'schen Regel

Hinweise

Hinzugefügt in Version 1.12.0.

Die zusammengesetzte Simpson'sche 1/3-Methode kann verwendet werden, um das bestimmte Integral einer abgetasteten Eingangsfunktion \(y(x)\) zu approximieren [1]. Die Methode nimmt eine quadratische Beziehung über dem Intervall an, das drei aufeinanderfolgende abgetastete Punkte umfasst.

Betrachten Sie drei aufeinanderfolgende Punkte: \((x_1, y_1), (x_2, y_2), (x_3, y_3)\).

Unter der Annahme einer quadratischen Beziehung über die drei Punkte ist das Integral über das Teilintervall zwischen \(x_1\) und \(x_2\) gegeben durch Formel (8) von [2]

\[\begin{split}\int_{x_1}^{x_2} y(x) dx\ &= \frac{x_2-x_1}{6}\left[\ \left\{3-\frac{x_2-x_1}{x_3-x_1}\right\} y_1 + \ \left\{3 + \frac{(x_2-x_1)^2}{(x_3-x_2)(x_3-x_1)} + \ \frac{x_2-x_1}{x_3-x_1}\right\} y_2\\ - \frac{(x_2-x_1)^2}{(x_3-x_2)(x_3-x_1)} y_3\right]\end{split}\]

Das Integral zwischen \(x_2\) und \(x_3\) ist gegeben, indem die Erscheinungen von \(x_1\) und \(x_3\) vertauscht werden. Das Integral wird für jedes Teilintervall separat geschätzt und dann kumulativ summiert, um das Endergebnis zu erhalten.

Für gleichmäßig verteilte Abtastwerte ist das Ergebnis exakt, wenn die Funktion ein Polynom vom Grad drei oder niedriger ist [1] und die Anzahl der Teilintervalle gerade ist. Andernfalls ist das Integral für Polynome vom Grad zwei oder niedriger exakt.

Referenzen

[1] (1,2)

Wikipedia-Seite: https://en.wikipedia.org/wiki/Simpson’s_rule

[2]

Cartwright, Kenneth V. Simpson’s Rule Cumulative Integration with MS Excel and Irregularly-spaced Data. Journal of Mathematical Sciences and Mathematics Education. 12 (2): 1-9

Beispiele

>>> from scipy import integrate
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(-2, 2, num=20)
>>> y = x**2
>>> y_int = integrate.cumulative_simpson(y, x=x, initial=0)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, y_int, 'ro', x, x**3/3 - (x[0])**3/3, 'b-')
>>> ax.grid()
>>> plt.show()

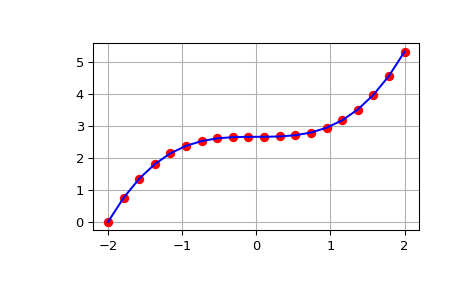
../../_images/scipy-integrate-cumulative_simpson-1_00_00.png

Die Ausgabe von cumulative_simpson ähnelt der von iterativem Aufrufen von simpson mit sukzessive höheren Integrationsgrenzen, ist aber nicht identisch.

>>> def cumulative_simpson_reference(y, x):
...     return np.asarray([integrate.simpson(y[:i], x=x[:i])
...                        for i in range(2, len(y) + 1)])
>>>
>>> rng = np.random.default_rng()
>>> x, y = rng.random(size=(2, 10))
>>> x.sort()
>>>
>>> res = integrate.cumulative_simpson(y, x=x)
>>> ref = cumulative_simpson_reference(y, x)
>>> equal = np.abs(res - ref) < 1e-15
>>> equal  # not equal when `simpson` has even number of subintervals
array([False,  True, False,  True, False,  True, False,  True,  True])

Dies ist zu erwarten: Da cumulative_simpson mehr Informationen zur Verfügung hat als simpson, kann es typischerweise genauere Schätzungen des zugrunde liegenden Integrals über Teilintervalle liefern.