scipy.signal.

Kohärenz#

scipy.signal.coherence(x, y, fs=1.0, window='hann', nperseg=None, noverlap=None, nfft=None, detrend='constant', axis=-1)[Quelle]#

Schätzt die betragsquadrierte Kohärenzschätzung, Cxy, von diskreten Zeitsignalen X und Y unter Verwendung der Welch-Methode.

Cxy = abs(Pxy)**2/(Pxx*Pyy), wobei Pxx und Pyy die Leistungsdichteschätzungen von X und Y sind und Pxy die Kreuzspektraldichteschätzung von X und Y ist.

Parameter:

xarray_like: Zeitreihen von Messwerten
yarray_like: Zeitreihen von Messwerten
fsfloat, optional: Abtastfrequenz der Zeitreihen x und y. Standardwert ist 1.0.
windowstr oder Tupel oder Array_like, optional: Gewünschtes Fenster zur Verwendung. Wenn window eine Zeichenkette oder ein Tupel ist, wird es an get_window übergeben, um die Fensterwerte zu generieren, die standardmäßig DFT-gerade sind. Siehe get_window für eine Liste von Fenstern und erforderliche Parameter. Wenn window Array_like ist, wird es direkt als Fenster verwendet und seine Länge muss nperseg sein. Standard ist ein Hann-Fenster.
npersegint, optional: Länge jedes Segments. Standard ist None, aber wenn window str oder tuple ist, wird es auf 256 gesetzt, und wenn window array_like ist, wird es auf die Länge des Fensters gesetzt.
noverlap: int, optional: Anzahl der Punkte, die zwischen Segmenten überlappt werden. Wenn None, dann noverlap = nperseg // 2. Standardwert ist None.
nfftint, optional: Länge der FFT, die verwendet wird, wenn eine Null-gepolsterte FFT gewünscht wird. Wenn None, ist die FFT-Länge nperseg. Standard ist None.
detrendstr oder Funktion oder False, optional: Gibt an, wie jedes Segment entzerrt werden soll. Wenn detrend eine Zeichenkette ist, wird sie als Argument type an die Funktion detrend übergeben. Wenn es sich um eine Funktion handelt, nimmt sie ein Segment entgegen und gibt ein entzerrtes Segment zurück. Wenn detrend False ist, wird keine Entzerrung durchgeführt. Standard ist 'constant'.
axisint, optional: Achse, entlang derer die Kohärenz für beide Eingaben berechnet wird; die Standardachse ist die letzte Achse (d. h. axis=-1).

Rückgabe:

fndarray: Array von Abtastfrequenzen.
Cxyndarray: Betragsquadrierte Kohärenz von x und y.

Siehe auch

periodogram: Einfaches, optional modifiziertes Periodogramm
lombscargle: Lomb-Scargle-Periodogramm für ungleichmäßig abgetastete Daten
welch: Leistungsdichteschätzung nach der Welch-Methode.
csd: Kreuzspektraldichteschätzung nach der Welch-Methode.

Hinweise

Ein angemessenes Maß für die Überlappung hängt von der Wahl des Fensters und Ihren Anforderungen ab. Für das Standard-Hann-Fenster ist eine Überlappung von 50 % ein vernünftiger Kompromiss zwischen der genauen Schätzung der Signalleistung und der Vermeidung von Mehrfachzählungen von Daten. Engere Fenster erfordern möglicherweise eine größere Überlappung.

Hinzugefügt in Version 0.16.0.

Referenzen

[1]

P. Welch, „The use of the fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms“, IEEE Trans. Audio Electroacoust. Bd. 15, S. 70-73, 1967.

[2]

Stoica, Petre und Randolph Moses, „Spectral Analysis of Signals“, Prentice Hall, 2005

Beispiele

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

Generieren Sie zwei Testsignale mit einigen gemeinsamen Merkmalen.

>>> fs = 10e3
>>> N = 1e5
>>> amp = 20
>>> freq = 1234.0
>>> noise_power = 0.001 * fs / 2
>>> time = np.arange(N) / fs
>>> b, a = signal.butter(2, 0.25, 'low')
>>> x = rng.normal(scale=np.sqrt(noise_power), size=time.shape)
>>> y = signal.lfilter(b, a, x)
>>> x += amp*np.sin(2*np.pi*freq*time)
>>> y += rng.normal(scale=0.1*np.sqrt(noise_power), size=time.shape)

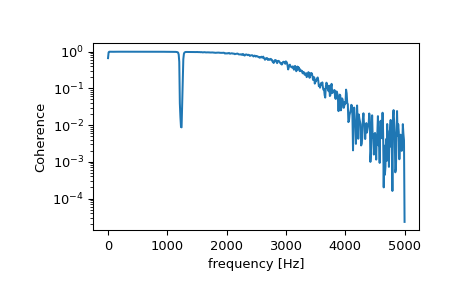
Berechnen und plotten Sie die Kohärenz.

>>> f, Cxy = signal.coherence(x, y, fs, nperseg=1024)
>>> plt.semilogy(f, Cxy)
>>> plt.xlabel('frequency [Hz]')
>>> plt.ylabel('Coherence')
>>> plt.show()

../../_images/scipy-signal-coherence-1.png