scipy.signal.

filtfilt

scipy.signal.filtfilt(b, a, x, axis=-1, padtype='odd', padlen=None, method='pad', irlen=None)

Wendet einen digitalen Filter vorwärts und rückwärts auf ein Signal an.

Diese Funktion wendet einen linearen digitalen Filter zweimal an, einmal vorwärts und einmal rückwärts. Der kombinierte Filter hat Null-Phase und eine doppelte Filterordnung des Originals.

Die Funktion bietet Optionen für die Behandlung der Signalränder.

Die Funktion sosfiltfilt (und Filterdesign mit output='sos') sollte für die meisten Filteraufgaben filtfilt vorgezogen werden, da Zweistufenfilter weniger numerische Probleme aufweisen.

Parameter:

b(N,) array_like

Der Zählerkoeffizientenvektor des Filters.

a(N,) array_like

Der Nennerkoeffizientenvektor des Filters. Wenn a[0] nicht 1 ist, werden sowohl a als auch b durch a[0] normalisiert.

xarray_like

Das Array der zu filternden Daten.

axisint, optional

Die Achse von x, auf die der Filter angewendet wird. Standard ist -1.

padtypestr oder None, optional

Muss ‘odd’, ‘even’, ‘constant’ oder None sein. Dies bestimmt die Art der Erweiterung, die für das aufgefüllte Signal verwendet wird, auf das der Filter angewendet wird. Wenn padtype None ist, wird keine Auffüllung verwendet. Standard ist ‘odd’.

padlenint oder None, optional

Die Anzahl der Elemente, um die x an beiden Enden der Achse axis erweitert wird, bevor der Filter angewendet wird. Dieser Wert muss kleiner sein als x.shape[axis] - 1. padlen=0 bedeutet keine Auffüllung. Der Standardwert ist 3 * max(len(a), len(b)).

methodstr, optional

Bestimmt die Methode zur Behandlung der Signalränder, entweder “pad” oder “gust”. Wenn method “pad” ist, wird das Signal aufgefüllt; die Art der Auffüllung wird durch padtype und padlen bestimmt, und irlen wird ignoriert. Wenn method “gust” ist, wird die Methode von Gustafsson verwendet und padtype und padlen werden ignoriert.

irlenint oder None, optional

Wenn method “gust” ist, gibt irlen die Länge der Impulsantwort des Filters an. Wenn irlen None ist, wird kein Teil der Impulsantwort ignoriert. Für ein langes Signal kann die Angabe von irlen die Leistung des Filters erheblich verbessern.

Rückgabe:

yndarray

Der gefilterte Ausgang mit der gleichen Form wie x.

Siehe auch

sosfiltfilt, lfilter_zi, lfilter, lfiltic, savgol_filter, sosfilt

Hinweise

Wenn method “pad” ist, füllt die Funktion die Daten entlang der angegebenen Achse auf drei Arten auf: ungerade, gerade oder konstant. Die ungeraden und geraden Erweiterungen haben die entsprechende Symmetrie zum Endpunkt der Daten. Die konstante Erweiterung erweitert die Daten mit den Werten an den Endpunkten. Sowohl im Vorwärts- als auch im Rückwärtsdurchlauf wird die Anfangsbedingung des Filters mithilfe von lfilter_zi gefunden und mit dem Endpunkt der erweiterten Daten skaliert.

Wenn method “gust” ist, wird die Methode von Gustafsson [1] verwendet. Die Anfangsbedingungen für den Vorwärts- und Rückwärtsdurchlauf werden so gewählt, dass der Vorwärts-Rückwärts-Filter das gleiche Ergebnis wie der Rückwärts-Vorwärts-Filter liefert.

Die Option zur Verwendung der Gustaffson-Methode wurde in der SciPy-Version 0.16.0 hinzugefügt.

Referenzen

[1]

F. Gustaffson, „Determining the initial states in forward-backward filtering“, Transactions on Signal Processing, Bd. 46, S. 988-992, 1996.

Beispiele

Probieren Sie es in Ihrem Browser aus!

Die Beispiele verwenden mehrere Funktionen aus scipy.signal.

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt

Zuerst erstellen wir ein einsekündiges Signal, das die Summe zweier reiner Sinuswellen mit Frequenzen von 5 Hz und 250 Hz ist, abgetastet mit 2000 Hz.

>>> t = np.linspace(0, 1.0, 2001)
>>> xlow = np.sin(2 * np.pi * 5 * t)
>>> xhigh = np.sin(2 * np.pi * 250 * t)
>>> x = xlow + xhigh

Erstellen Sie nun einen Tiefpass-Butterworth-Filter mit einer Grenzfrequenz von 0,125 mal der Nyquist-Frequenz oder 125 Hz, und wenden Sie ihn mit filtfilt auf x an. Das Ergebnis sollte ungefähr xlow entsprechen, ohne Phasenverschiebung.

>>> b, a = signal.butter(8, 0.125)
>>> y = signal.filtfilt(b, a, x, padlen=150)
>>> np.abs(y - xlow).max()
9.1086182074789912e-06

Wir erhalten ein ziemlich sauberes Ergebnis für dieses künstliche Beispiel, da die ungerade Erweiterung exakt ist und die Transienten des Filters mit der moderat langen Auffüllung abklingen, bevor die eigentlichen Daten erreicht werden. Im Allgemeinen sind Transienteneffekte an den Rändern unvermeidlich.

Das folgende Beispiel demonstriert die Option method="gust".

Erstellen Sie zuerst einen Filter.

>>> b, a = signal.ellip(4, 0.01, 120, 0.125)  # Filter to be applied.

sig ist ein zufälliges Eingangssignal, das gefiltert werden soll.

>>> rng = np.random.default_rng()
>>> n = 60
>>> sig = rng.standard_normal(n)**3 + 3*rng.standard_normal(n).cumsum()

Wenden Sie filtfilt auf sig an, einmal mit der Gustafsson-Methode und einmal mit Auffüllung, und plotten Sie die Ergebnisse zum Vergleich.

>>> fgust = signal.filtfilt(b, a, sig, method="gust")
>>> fpad = signal.filtfilt(b, a, sig, padlen=50)
>>> plt.plot(sig, 'k-', label='input')
>>> plt.plot(fgust, 'b-', linewidth=4, label='gust')
>>> plt.plot(fpad, 'c-', linewidth=1.5, label='pad')
>>> plt.legend(loc='best')
>>> plt.show()

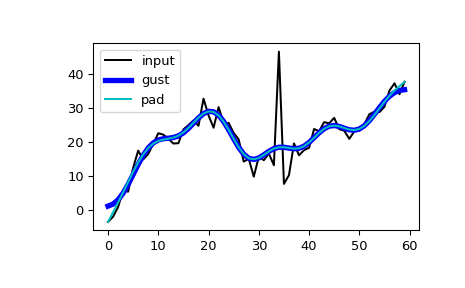
Das Argument irlen kann verwendet werden, um die Leistung der Gustafsson-Methode zu verbessern.

Schätzen Sie die Länge der Impulsantwort des Filters ab.

>>> z, p, k = signal.tf2zpk(b, a)
>>> eps = 1e-9
>>> r = np.max(np.abs(p))
>>> approx_impulse_len = int(np.ceil(np.log(eps) / np.log(r)))
>>> approx_impulse_len
137

Wenden Sie den Filter auf ein längeres Signal an, mit und ohne das Argument irlen. Der Unterschied zwischen y1 und y2 ist gering. Für lange Signale bietet die Verwendung von irlen eine signifikante Leistungsverbesserung.

>>> x = rng.standard_normal(4000)
>>> y1 = signal.filtfilt(b, a, x, method='gust')
>>> y2 = signal.filtfilt(b, a, x, method='gust', irlen=approx_impulse_len)
>>> print(np.max(np.abs(y1 - y2)))
2.875334415008979e-10

ZurückIn Tab öffnen