scipy.signal.

sosfiltfilt

scipy.signal.sosfiltfilt(sos, x, axis=-1, padtype='odd', padlen=None)

Ein vorwärts-rückwärts gerichteter digitaler Filter unter Verwendung von kaskadierten Filtersektionen zweiter Ordnung.

Siehe filtfilt für umfassendere Informationen zu dieser Methode.

Parameter:

sosarray_like

Array von Koeffizienten von Filtersektionen zweiter Ordnung, muss die Form (n_sections, 6) haben. Jede Zeile entspricht einer Filtersektion zweiter Ordnung, wobei die ersten drei Spalten die Zählerkoeffizienten und die letzten drei die Nennerkoeffizienten liefern.

xarray_like

Das Array der zu filternden Daten.

axisint, optional

Die Achse von x, auf die der Filter angewendet wird. Standard ist -1.

padtypestr oder None, optional

Muss ‘odd’, ‘even’, ‘constant’ oder None sein. Dies bestimmt die Art der Erweiterung, die für das aufgefüllte Signal verwendet wird, auf das der Filter angewendet wird. Wenn padtype None ist, wird keine Auffüllung verwendet. Der Standardwert ist ‘odd’.

padlenint oder None, optional

Die Anzahl der Elemente, um die x an beiden Enden der Achse axis erweitert wird, bevor der Filter angewendet wird. Dieser Wert muss kleiner als x.shape[axis] - 1 sein. padlen=0 impliziert keine Auffüllung. Der Standardwert ist

3 * (2 * len(sos) + 1 - min((sos[:, 2] == 0).sum(),
                            (sos[:, 5] == 0).sum()))

Die zusätzliche Subtraktion am Ende versucht, Pole und Nullen am Ursprung (z.B. bei Filtern ungerader Ordnung) zu kompensieren, um äquivalente Schätzungen von padlen zu erzielen, wie sie filtfilt für Filter zweiter Ordnung bietet, die mit Funktionen von scipy.signal erstellt wurden.

Rückgabe:

yndarray

Die gefilterte Ausgabe mit der gleichen Form wie x.

Siehe auch

filtfilt, sosfilt, sosfilt_zi, freqz_sos

Hinweise

Hinzugefügt in Version 0.18.0.

Beispiele

Probieren Sie es in Ihrem Browser aus!

>>> import numpy as np
>>> from scipy.signal import sosfiltfilt, butter
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

Erstellen eines interessanten Signals zum Filtern.

>>> n = 201
>>> t = np.linspace(0, 1, n)
>>> x = 1 + (t < 0.5) - 0.25*t**2 + 0.05*rng.standard_normal(n)

Erstellen Sie einen Tiefpass-Butterworth-Filter und verwenden Sie ihn, um x zu filtern.

>>> sos = butter(4, 0.125, output='sos')
>>> y = sosfiltfilt(sos, x)

Zum Vergleich wird ein Filter 8. Ordnung mit sosfilt angewendet. Der Filter wird mit dem Mittelwert der ersten vier Werte von x initialisiert.

>>> from scipy.signal import sosfilt, sosfilt_zi
>>> sos8 = butter(8, 0.125, output='sos')
>>> zi = x[:4].mean() * sosfilt_zi(sos8)
>>> y2, zo = sosfilt(sos8, x, zi=zi)

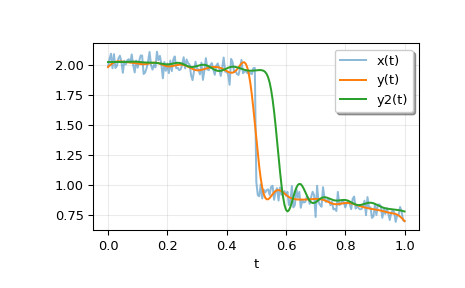
Plotten Sie die Ergebnisse. Beachten Sie, dass die Phase von y mit der Eingabe übereinstimmt, während y2 eine signifikante Phasenverzögerung aufweist.

>>> plt.plot(t, x, alpha=0.5, label='x(t)')
>>> plt.plot(t, y, label='y(t)')
>>> plt.plot(t, y2, label='y2(t)')
>>> plt.legend(framealpha=1, shadow=True)
>>> plt.grid(alpha=0.25)
>>> plt.xlabel('t')
>>> plt.show()

ZurückIn Tab öffnen