scipy.special.erf#
- scipy.special.erf(z, out=None) = <ufunc 'erf'>#
Gibt die Fehlerfunktion für komplexe Argumente zurück.
Sie ist definiert als
2/sqrt(pi)*integral(exp(-t**2), t=0..z).- Parameter:
- xndarray
Eingabearray.
- outndarray, optional
Optionales Ausgabe-Array für die Funktionswerte
- Rückgabe:
- resSkalar oder ndarray
Die Werte der Fehlerfunktion an den gegebenen Punkten x.
Hinweise
Die kumulative Verteilungsfunktion der Standardnormalverteilung ist gegeben durch
Phi(z) = 1/2[1 + erf(z/sqrt(2))].erfhat experimentelle Unterstützung für Backends, die mit der Python Array API Standard kompatibel sind, zusätzlich zu NumPy. Bitte erwägen Sie, diese Funktionen zu testen, indem Sie eine UmgebungsvariableSCIPY_ARRAY_API=1setzen und CuPy-, PyTorch-, JAX- oder Dask-Arrays als Array-Argumente bereitstellen. Die folgenden Kombinationen von Backend und Gerät (oder anderer Fähigkeit) werden unterstützt.Bibliothek
CPU
GPU
NumPy
✅
n/a
CuPy
n/a
✅
PyTorch
✅
✅
JAX
✅
✅
Dask
✅
n/a
Siehe Unterstützung für den Array API Standard für weitere Informationen.
Referenzen
[2]Milton Abramowitz und Irene A. Stegun, Hrsg. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. http://www.math.sfu.ca/~cbm/aands/page_297.htm
[3]Steven G. Johnson, Faddeeva W-Funktionsimplementierung. http://ab-initio.mit.edu/Faddeeva
Beispiele
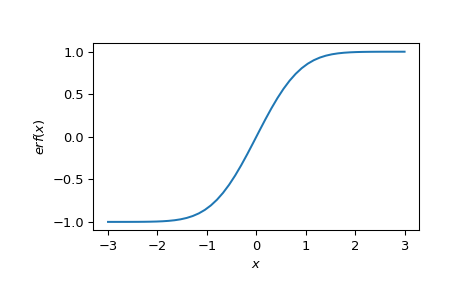
>>> import numpy as np >>> from scipy import special >>> import matplotlib.pyplot as plt >>> x = np.linspace(-3, 3) >>> plt.plot(x, special.erf(x)) >>> plt.xlabel('$x$') >>> plt.ylabel('$erf(x)$') >>> plt.show()