scipy.special.eval_legendre#

scipy.special.eval_legendre(n, x, out=None) = <ufunc 'eval_legendre'>#

Legendre-Polynom an einem Punkt auswerten.

Die Legendre-Polynome können über die Gauss'sche hypergeometrische Funktion \({}_2F_1\) definiert werden als

\[P_n(x) = {}_2F_1(-n, n + 1; 1; (1 - x)/2).\]

Wenn \(n\) eine ganze Zahl ist, ist das Ergebnis ein Polynom vom Grad \(n\). Siehe 22.5.49 in [AS] für Details.

Parameter:

narray_like: Grad des Polynoms. Wenn keine ganze Zahl, wird das Ergebnis über den Zusammenhang mit der Gaußschen hypergeometrischen Funktion bestimmt.
xarray_like: Punkte, an denen das Legendre-Polynom ausgewertet werden soll
outndarray, optional: Optionales Ausgabe-Array für die Funktionswerte

Rückgabe:

PSkalar oder ndarray: Werte des Legendre-Polynoms

Siehe auch

roots_legendre: Wurzeln und Quadratur-Gewichte von Legendre-Polynomen
legendre: Legendre-Polynom-Objekt
hyp2f1: Gaußsche hypergeometrische Funktion
numpy.polynomial.legendre.Legendre: Legendre-Reihe

Referenzen

[AS]

Milton Abramowitz und Irene A. Stegun, Hrsg. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972.

Beispiele

>>> import numpy as np
>>> from scipy.special import eval_legendre

Auswertung des Legendre-Polynoms nullter Ordnung an x = 0

>>> eval_legendre(0, 0)
1.0

Auswertung des Legendre-Polynoms erster Ordnung zwischen -1 und 1

>>> X = np.linspace(-1, 1, 5)  # Domain of Legendre polynomials
>>> eval_legendre(1, X)
array([-1. , -0.5,  0. ,  0.5,  1. ])

Auswertung von Legendre-Polynomen der Ordnungen 0 bis 4 an x = 0

>>> N = range(0, 5)
>>> eval_legendre(N, 0)
array([ 1.   ,  0.   , -0.5  ,  0.   ,  0.375])

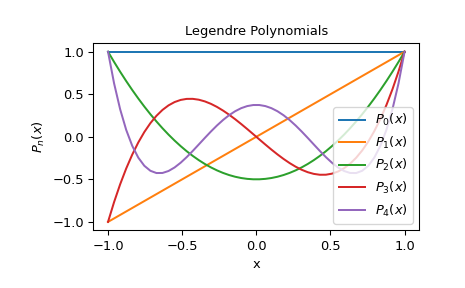
Zeichnen von Legendre-Polynomen der Ordnungen 0 bis 4

>>> X = np.linspace(-1, 1)

>>> import matplotlib.pyplot as plt
>>> for n in range(0, 5):
...     y = eval_legendre(n, X)
...     plt.plot(X, y, label=r'$P_{}(x)$'.format(n))

>>> plt.title("Legendre Polynomials")
>>> plt.xlabel("x")
>>> plt.ylabel(r'$P_n(x)$')
>>> plt.legend(loc='lower right')
>>> plt.show()

../../_images/scipy-special-eval_legendre-1.png