genlaguerre#
- scipy.special.genlaguerre(n, alpha, monic=False)[Quellcode]#
Verallgemeinertes (assoziiertes) Laguerre-Polynom.
Definiert als die Lösung von
\[x\frac{d^2}{dx^2}L_n^{(\alpha)} + (\alpha + 1 - x)\frac{d}{dx}L_n^{(\alpha)} + nL_n^{(\alpha)} = 0,\]wobei \(\alpha > -1\); \(L_n^{(\alpha)}\) ein Polynom vom Grad \(n\) ist.
- Parameter:
- nint
Grad des Polynoms.
- alphafloat
Parameter, muss größer als -1 sein.
- monicbool, optional
Wenn True, wird der führende Koeffizient auf 1 skaliert. Standard ist False.
- Rückgabe:
- Lorthopoly1d
Allgemeines Laguerre-Polynom.
Hinweise
Für festes \(\alpha\) sind die Polynome \(L_n^{(\alpha)}\) orthogonal über \([0, \infty)\) mit der Gewichtsfunktion \(e^{-x}x^\alpha\).
Die Laguerre-Polynome sind der Spezialfall, bei dem \(\alpha = 0\) ist.
Referenzen
[AS]Milton Abramowitz und Irene A. Stegun, Hrsg. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972.
Beispiele
Die verallgemeinerten Laguerre-Polynome stehen in engem Zusammenhang mit der konfluenten hypergeometrischen Funktion \({}_1F_1\)
\[L_n^{(\alpha)} = \binom{n + \alpha}{n} {}_1F_1(-n, \alpha +1, x)\]Dies kann zum Beispiel für \(n = \alpha = 3\) über das Intervall \([-1, 1]\) verifiziert werden
>>> import numpy as np >>> from scipy.special import binom >>> from scipy.special import genlaguerre >>> from scipy.special import hyp1f1 >>> x = np.arange(-1.0, 1.0, 0.01) >>> np.allclose(genlaguerre(3, 3)(x), binom(6, 3) * hyp1f1(-3, 4, x)) True
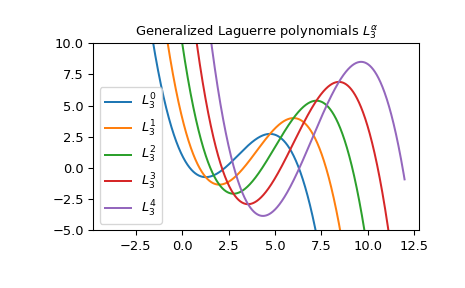
Dies ist die Darstellung der verallgemeinerten Laguerre-Polynome \(L_3^{(\alpha)}\) für einige Werte von \(\alpha\)
>>> import matplotlib.pyplot as plt >>> x = np.arange(-4.0, 12.0, 0.01) >>> fig, ax = plt.subplots() >>> ax.set_ylim(-5.0, 10.0) >>> ax.set_title(r'Generalized Laguerre polynomials $L_3^{\alpha}$') >>> for alpha in np.arange(0, 5): ... ax.plot(x, genlaguerre(3, alpha)(x), label=rf'$L_3^{(alpha)}$') >>> plt.legend(loc='best') >>> plt.show()