scipy.special.ive#
- scipy.special.ive(v, z, out=None) = <ufunc 'ive'>#
Exponentiell skalierte modifizierte Besselfunktion erster Art.
Definiert als
ive(v, z) = iv(v, z) * exp(-abs(z.real))
Für imaginäre Zahlen ohne Realteil wird die unskalierte Besselfunktion erster Art
ivzurückgegeben.- Parameter:
- varray_like of float
Ordnung.
- zarray_like von float oder complex
Argument.
- outndarray, optional
Optionales Ausgabe-Array für die Funktionswerte
- Rückgabe:
- skalar oder ndarray
Werte der exponentiell skalierten modifizierten Besselfunktion.
Siehe auch
Hinweise
Für positives v wird die AMOS [1] zbesi Routine aufgerufen. Sie verwendet eine Potenzreihe für kleine z, die asymptotische Entwicklung für große abs(z), den Miller-Algorithmus normalisiert durch das Wronskion und eine Neumann-Reihe für mittlere Beträge sowie die uniforme asymptotische Entwicklung für \(I_v(z)\) und \(J_v(z)\) für große Ordnungen. Rückwärtsrekursion wird verwendet, um Sequenzen zu generieren oder Ordnungen bei Bedarf zu reduzieren.
Die obigen Berechnungen werden in der rechten Halbebene durchgeführt und durch die Formel in die linke Halbebene fortgesetzt,
\[I_v(z \exp(\pm\imath\pi)) = \exp(\pm\pi v) I_v(z)\](gültig, wenn der Realteil von z positiv ist). Für negatives v wird die Formel
\[I_{-v}(z) = I_v(z) + \frac{2}{\pi} \sin(\pi v) K_v(z)\]verwendet, wobei \(K_v(z)\) die modifizierte Besselfunktion zweiter Art ist, ausgewertet mit der AMOS Routine zbesk.
iveist nützlich für große Argumente z: für diese überläuftivleicht, währendiveaufgrund der exponentiellen Skalierung nicht überläuft.Referenzen
[1]Donald E. Amos, „AMOS, A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order“, http://netlib.org/amos/
Beispiele
Im folgenden Beispiel gibt
ivUnendlich zurück, währendiveimmer noch eine endliche Zahl zurückgibt.>>> from scipy.special import iv, ive >>> import numpy as np >>> import matplotlib.pyplot as plt >>> iv(3, 1000.), ive(3, 1000.) (inf, 0.01256056218254712)
Werten Sie die Funktion an einem Punkt für verschiedene Ordnungen aus, indem Sie eine Liste oder ein NumPy-Array als Argument für den Parameter v angeben
>>> ive([0, 1, 1.5], 1.) array([0.46575961, 0.20791042, 0.10798193])
Auswertung der Funktion an mehreren Punkten für Ordnung 0 durch Übergabe eines Arrays für z.
>>> points = np.array([-2., 0., 3.]) >>> ive(0, points) array([0.30850832, 1. , 0.24300035])
Werten Sie die Funktion an mehreren Punkten für verschiedene Ordnungen aus, indem Sie Arrays sowohl für v als auch für z angeben. Beide Arrays müssen so erweiterbar sein, dass sie die richtige Form erhalten. Um die Ordnungen 0, 1 und 2 für ein 1D-Array von Punkten zu berechnen
>>> ive([[0], [1], [2]], points) array([[ 0.30850832, 1. , 0.24300035], [-0.21526929, 0. , 0.19682671], [ 0.09323903, 0. , 0.11178255]])
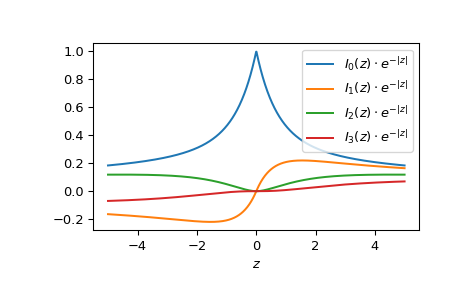
Plotten Sie die Funktionen der Ordnungen 0 bis 3 von -5 bis 5.
>>> fig, ax = plt.subplots() >>> x = np.linspace(-5., 5., 1000) >>> for i in range(4): ... ax.plot(x, ive(i, x), label=fr'$I_{i!r}(z)\cdot e^{{-|z|}}$') >>> ax.legend() >>> ax.set_xlabel(r"$z$") >>> plt.show()