scipy.special.

jnp_zeros

scipy.special.jnp_zeros(n, nt)

Berechnet Nullstellen von Bessel-Funktionsderivaten Jn’ ganzzahliger Ordnung.

Berechnet nt Nullstellen der Funktionen \(J_n'(x)\) im Intervall \((0, \infty)\). Die Nullstellen werden in aufsteigender Reihenfolge zurückgegeben. Beachten Sie, dass dieses Intervall die Nullstelle bei \(x = 0\) ausschließt, die für \(n > 1\) existiert.

Parameter:

nint

Ordnung der Bessel-Funktion

ntint

Anzahl der zurückzugebenden Nullstellen

Rückgabe:

ndarray

Erste nt Nullstellen der Bessel-Funktion.

Siehe auch

jvp

Ableitungen von Bessel-Funktionen der ersten Art ganzzahliger Ordnung

jv

Bessel-Funktionen der ersten Art mit reeller Ordnung

Referenzen

[1]

Zhang, Shanjie und Jin, Jianming. „Computation of Special Functions“, John Wiley and Sons, 1996, Kapitel 5. https://people.sc.fsu.edu/~jburkardt/f77_src/special_functions/special_functions.html

Beispiele

Probieren Sie es in Ihrem Browser aus!

Berechnet die ersten vier Wurzeln von \(J_2'\).

>>> from scipy.special import jnp_zeros
>>> jnp_zeros(2, 4)
array([ 3.05423693,  6.70613319,  9.96946782, 13.17037086])

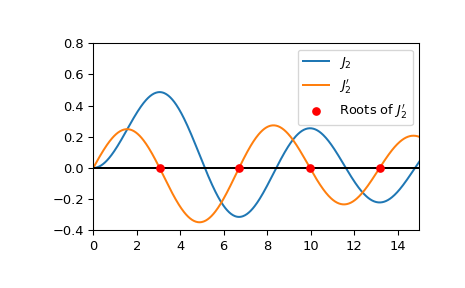
Da jnp_zeros die Wurzeln von \(J_n'\) liefert, kann es verwendet werden, um die Positionen der Maxima von \(J_n\) zu berechnen. Plottet \(J_2\), \(J_2'\) und die Positionen der Wurzeln von \(J_2'\).

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.special import jn, jnp_zeros, jvp
>>> j2_roots = jnp_zeros(2, 4)
>>> xmax = 15
>>> x = np.linspace(0, xmax, 500)
>>> fig, ax = plt.subplots()
>>> ax.plot(x, jn(2, x), label=r'$J_2$')
>>> ax.plot(x, jvp(2, x, 1), label=r"$J_2'$")
>>> ax.hlines(0, 0, xmax, color='k')
>>> ax.scatter(j2_roots, np.zeros((4, )), s=30, c='r',
...            label=r"Roots of $J_2'$", zorder=5)
>>> ax.set_ylim(-0.4, 0.8)
>>> ax.set_xlim(0, xmax)
>>> plt.legend()
>>> plt.show()

ZurückIn Tab öffnen