scipy.special.jv#

scipy.special.jv(v, z, out=None) = <ufunc 'jv'>#

Bessel-Funktion erster Art von reeller Ordnung und komplexem Argument.

Parameter:

varray_like: Ordnung (float).
zarray_like: Argument (float oder komplex).
outndarray, optional: Optionales Ausgabe-Array für die Funktionswerte

Rückgabe:

JSkalar oder ndarray: Wert der Bessel-Funktion, \(J_v(z)\).

Siehe auch

jve: \(J_v\) mit abgetrennter führender exponentieller Verhaltensweise.
spherical_jn: Sphärische Bessel-Funktionen.
j0: schnellere Version dieser Funktion für Ordnung 0.
j1: schnellere Version dieser Funktion für Ordnung 1.

Hinweise

Für positive v Werte wird die Berechnung mit der AMOS [1] zbesj Routine durchgeführt, die die Verbindung zur modifizierten Bessel-Funktion \(I_v\) nutzt,

\[ \begin{align}\begin{aligned}J_v(z) = \exp(v\pi\imath/2) I_v(-\imath z)\qquad (\Im z > 0)\\J_v(z) = \exp(-v\pi\imath/2) I_v(\imath z)\qquad (\Im z < 0)\end{aligned}\end{align} \]

Für negative v-Werte wird die Formel,

\[J_{-v}(z) = J_v(z) \cos(\pi v) - Y_v(z) \sin(\pi v)\]

verwendet wird, wobei \(Y_v(z)\) die Bessel-Funktion zweiter Art ist, berechnet mit der AMOS-Routine zbesy. Beachten Sie, dass der zweite Term für ganzzahlige v exakt Null ist; um die Genauigkeit zu verbessern, wird der zweite Term für v Werte, so dass v = floor(v), explizit weggelassen.

Nicht zu verwechseln mit den sphärischen Bessel-Funktionen (siehe spherical_jn).

Referenzen

[1]

Donald E. Amos, „AMOS, A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order“, http://netlib.org/amos/

Beispiele

Auswertung der Funktion der Ordnung 0 an einem Punkt.

>>> from scipy.special import jv
>>> jv(0, 1.)
0.7651976865579666

Auswertung der Funktion an einem Punkt für verschiedene Ordnungen.

>>> jv(0, 1.), jv(1, 1.), jv(1.5, 1.)
(0.7651976865579666, 0.44005058574493355, 0.24029783912342725)

Die Auswertung für verschiedene Ordnungen kann in einem Aufruf erfolgen, indem eine Liste oder ein NumPy-Array als Argument für den Parameter v übergeben wird.

>>> jv([0, 1, 1.5], 1.)
array([0.76519769, 0.44005059, 0.24029784])

Auswertung der Funktion an mehreren Punkten für Ordnung 0 durch Übergabe eines Arrays für z.

>>> import numpy as np
>>> points = np.array([-2., 0., 3.])
>>> jv(0, points)
array([ 0.22389078,  1.        , -0.26005195])

Wenn z ein Array ist, muss der Ordnungs-Parameter v so broadcastfähig sein, dass die korrekte Form entsteht, wenn in einem Aufruf unterschiedliche Ordnungen berechnet werden sollen. Um die Ordnungen 0 und 1 für ein 1D-Array zu berechnen

>>> orders = np.array([[0], [1]])
>>> orders.shape
(2, 1)

>>> jv(orders, points)
array([[ 0.22389078,  1.        , -0.26005195],
       [-0.57672481,  0.        ,  0.33905896]])

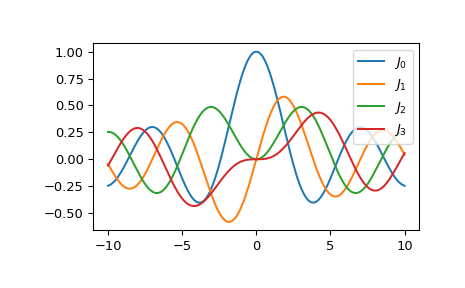
Zeichnen Sie die Funktionen der Ordnung 0 bis 3 von -10 bis 10.

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> x = np.linspace(-10., 10., 1000)
>>> for i in range(4):
...     ax.plot(x, jv(i, x), label=f'$J_{i!r}$')
>>> ax.legend()
>>> plt.show()