scipy.special.nbdtr#

scipy.special.nbdtr(k, n, p, out=None) = <ufunc 'nbdtr'>#

Negative binomial kumulative Verteilungsfunktion.

Gibt die Summe der Terme 0 bis k der negativen Binomialverteilungs-Wahrscheinlichkeitsmassenfunktion zurück,

\[F = \sum_{j=0}^k {{n + j - 1}\choose{j}} p^n (1 - p)^j.\]

In einer Folge von Bernoulli-Versuchen mit individuellen Erfolgswahrscheinlichkeiten p ist dies die Wahrscheinlichkeit, dass k oder weniger Misserfolge dem nth Erfolg vorausgehen.

Parameter:

karray_like: Die maximal zulässige Anzahl von Fehlschlägen (nicht-negative Ganzzahl).
narray_like: Die Zielanzahl von Erfolgen (positive Ganzzahl).
parray_like: Wahrscheinlichkeit eines Erfolgs bei einem einzelnen Ereignis (float).
outndarray, optional: Optionales Ausgabe-Array für die Funktionsergebnisse

Rückgabe:

FSkalar oder ndarray: Die Wahrscheinlichkeit von k oder weniger Misserfolgen vor n Erfolgen in einer Folge von Ereignissen mit individueller Erfolgswahrscheinlichkeit p.

Siehe auch

nbdtrc: Negative binomial Überlebensfunktion
nbdtrik: Negative binomial Quantilfunktion
scipy.stats.nbinom: Binomialverteilung (negativ)

Hinweise

Wenn Gleitkommazahlen für k oder n übergeben werden, werden diese auf ganze Zahlen gekürzt.

Die Terme werden nicht direkt summiert; stattdessen wird die regularisierte unvollständige Betafunktion gemäß der Formel verwendet:

\[\mathrm{nbdtr}(k, n, p) = I_{p}(n, k + 1).\]

Wrapper für die Cephes [1] Routine nbdtr.

Die negative Binomialverteilung ist auch als scipy.stats.nbinom verfügbar. Die direkte Verwendung von nbdtr kann die Leistung im Vergleich zur cdf Methode von scipy.stats.nbinom verbessern (siehe letztes Beispiel).

Referenzen

[1]

Cephes Mathematical Functions Library, http://www.netlib.org/cephes/

Beispiele

Berechnung der Funktion für k=10 und n=5 bei p=0.5.

>>> import numpy as np
>>> from scipy.special import nbdtr
>>> nbdtr(10, 5, 0.5)
0.940765380859375

Berechnung der Funktion für n=10 und p=0.5 an mehreren Punkten durch Übergabe eines NumPy-Arrays oder einer Liste für k.

>>> nbdtr([5, 10, 15], 10, 0.5)
array([0.15087891, 0.58809853, 0.88523853])

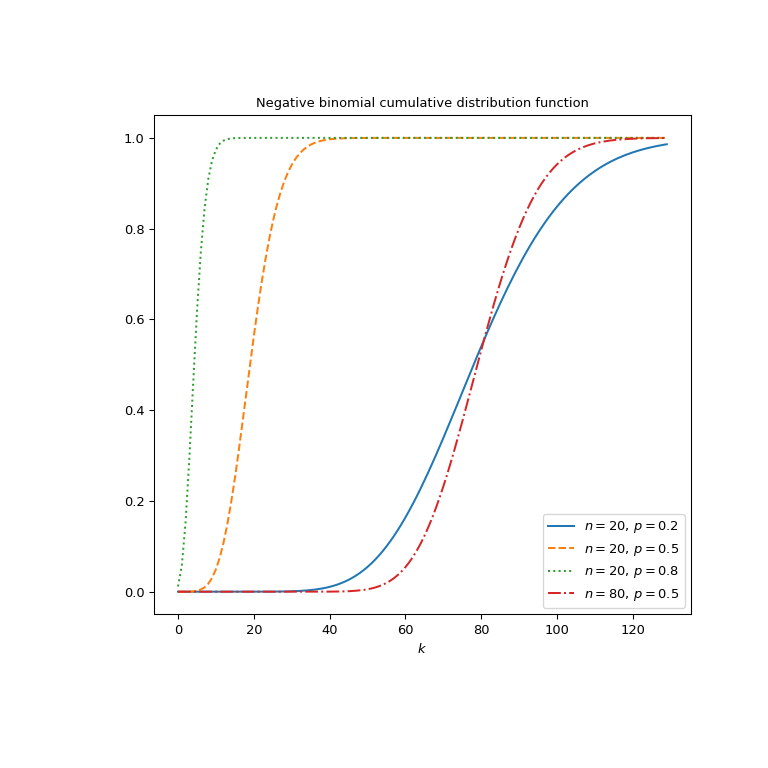
Plotten der Funktion für vier verschiedene Parametersätze.

>>> import matplotlib.pyplot as plt
>>> k = np.arange(130)
>>> n_parameters = [20, 20, 20, 80]
>>> p_parameters = [0.2, 0.5, 0.8, 0.5]
>>> linestyles = ['solid', 'dashed', 'dotted', 'dashdot']
>>> parameters_list = list(zip(p_parameters, n_parameters,
...                            linestyles))
>>> fig, ax = plt.subplots(figsize=(8, 8))
>>> for parameter_set in parameters_list:
...     p, n, style = parameter_set
...     nbdtr_vals = nbdtr(k, n, p)
...     ax.plot(k, nbdtr_vals, label=rf"$n={n},\, p={p}$",
...             ls=style)
>>> ax.legend()
>>> ax.set_xlabel("$k$")
>>> ax.set_title("Negative binomial cumulative distribution function")
>>> plt.show()

../../_images/scipy-special-nbdtr-1_00_00.png

Die negative Binomialverteilung ist auch als scipy.stats.nbinom verfügbar. Die direkte Verwendung von nbdtr kann deutlich schneller sein als der Aufruf der cdf Methode von scipy.stats.nbinom, insbesondere für kleine Arrays oder einzelne Werte. Um dieselben Ergebnisse zu erzielen, muss die folgende Parametrisierung verwendet werden: nbinom(n, p).cdf(k)=nbdtr(k, n, p).

>>> from scipy.stats import nbinom
>>> k, n, p = 5, 3, 0.5
>>> nbdtr_res = nbdtr(k, n, p)  # this will often be faster than below
>>> stats_res = nbinom(n, p).cdf(k)
>>> stats_res, nbdtr_res  # test that results are equal
(0.85546875, 0.85546875)

nbdtr kann verschiedene Parametersätze auswerten, indem Arrays mit für Broadcasting kompatiblen Formen für k, n und p übergeben werden. Hier berechnen wir die Funktion für drei verschiedene k an vier Stellen p, was zu einem 3x4-Array führt.

>>> k = np.array([[5], [10], [15]])
>>> p = np.array([0.3, 0.5, 0.7, 0.9])
>>> k.shape, p.shape
((3, 1), (4,))

>>> nbdtr(k, 5, p)
array([[0.15026833, 0.62304687, 0.95265101, 0.9998531 ],
       [0.48450894, 0.94076538, 0.99932777, 0.99999999],
       [0.76249222, 0.99409103, 0.99999445, 1.        ]])