scipy.special.nbdtrc#
- scipy.special.nbdtrc(k, n, p, out=None) = <ufunc 'nbdtrc'>#
Überlebensfunktion der negativen Binomialverteilung.
Gibt die Summe der Terme k + 1 bis unendlich der Wahrscheinlichkeitsmassenfunktion der negativen Binomialverteilung zurück:
\[F = \sum_{j=k + 1}^\infty {{n + j - 1}\choose{j}} p^n (1 - p)^j.\]In einer Folge von Bernoulli-Versuchen mit individueller Erfolgswahrscheinlichkeit p ist dies die Wahrscheinlichkeit, dass mehr als k Misserfolge dem nth Erfolg vorausgehen.
- Parameter:
- karray_like
Die maximal zulässige Anzahl von Fehlschlägen (nicht-negative Ganzzahl).
- narray_like
Die Zielanzahl von Erfolgen (positive Ganzzahl).
- parray_like
Wahrscheinlichkeit eines Erfolgs bei einem einzelnen Ereignis (float).
- outndarray, optional
Optionales Ausgabe-Array für die Funktionsergebnisse
- Rückgabe:
- FSkalar oder ndarray
Die Wahrscheinlichkeit von k + 1 oder mehr Misserfolgen vor n Erfolgen in einer Folge von Ereignissen mit individueller Erfolgswahrscheinlichkeit p.
Siehe auch
nbdtrNegative Binomial kumulative Verteilungsfunktion
nbdtrikNegative Binomial Perzentilfunktion
scipy.stats.nbinomBinomialverteilung (negativ)
Hinweise
Wenn Gleitkommazahlen für k oder n übergeben werden, werden sie auf ganze Zahlen gekürzt.
Die Terme werden nicht direkt summiert; stattdessen wird die regularisierte unvollständige Betafunktion gemäß der Formel verwendet:
\[\mathrm{nbdtrc}(k, n, p) = I_{1 - p}(k + 1, n).\]Wrapper für die Cephes [1] Routine
nbdtrc.Die negative Binomialverteilung ist auch als
scipy.stats.nbinomverfügbar. Die direkte Verwendung vonnbdtrckann die Leistung im Vergleich zursf-Methode vonscipy.stats.nbinomverbessern (siehe letztes Beispiel).Referenzen
[1]Cephes Mathematical Functions Library, http://www.netlib.org/cephes/
Beispiele
Berechnen Sie die Funktion für
k=10undn=5beip=0.5.>>> import numpy as np >>> from scipy.special import nbdtrc >>> nbdtrc(10, 5, 0.5) 0.059234619140624986
Berechnen Sie die Funktion für
n=10undp=0.5an mehreren Punkten, indem Sie ein NumPy-Array oder eine Liste für k bereitstellen.>>> nbdtrc([5, 10, 15], 10, 0.5) array([0.84912109, 0.41190147, 0.11476147])
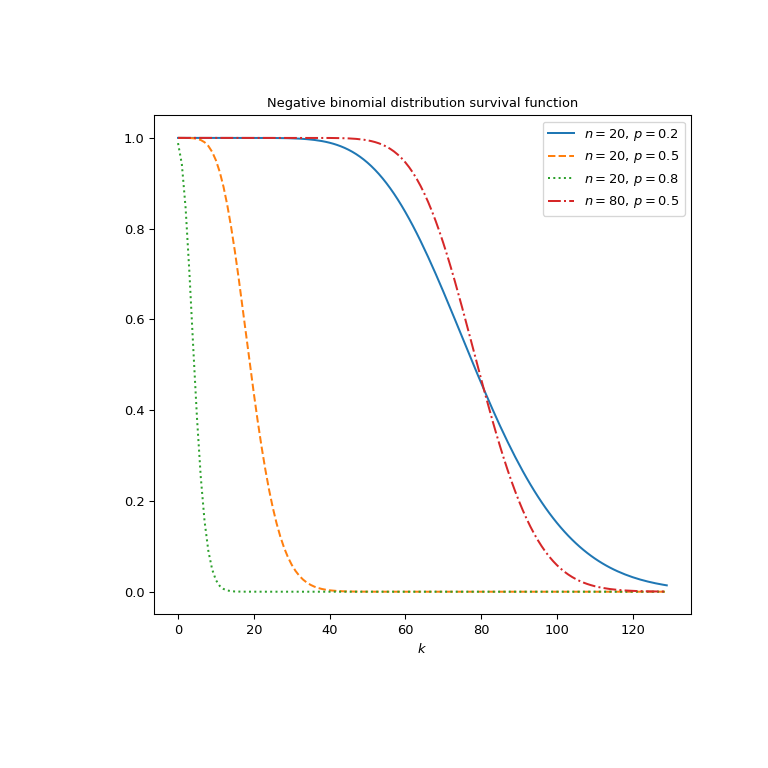
Plotten der Funktion für vier verschiedene Parametersätze.
>>> import matplotlib.pyplot as plt >>> k = np.arange(130) >>> n_parameters = [20, 20, 20, 80] >>> p_parameters = [0.2, 0.5, 0.8, 0.5] >>> linestyles = ['solid', 'dashed', 'dotted', 'dashdot'] >>> parameters_list = list(zip(p_parameters, n_parameters, ... linestyles)) >>> fig, ax = plt.subplots(figsize=(8, 8)) >>> for parameter_set in parameters_list: ... p, n, style = parameter_set ... nbdtrc_vals = nbdtrc(k, n, p) ... ax.plot(k, nbdtrc_vals, label=rf"$n={n},\, p={p}$", ... ls=style) >>> ax.legend() >>> ax.set_xlabel("$k$") >>> ax.set_title("Negative binomial distribution survival function") >>> plt.show()
Die negative Binomialverteilung ist auch als
scipy.stats.nbinomverfügbar. Die direkte Verwendung vonnbdtrckann wesentlich schneller sein als der Aufruf dersf-Methode vonscipy.stats.nbinom, insbesondere für kleine Arrays oder einzelne Werte. Um dieselben Ergebnisse zu erhalten, muss die folgende Parametrisierung verwendet werden:nbinom(n, p).sf(k)=nbdtrc(k, n, p).>>> from scipy.stats import nbinom >>> k, n, p = 3, 5, 0.5 >>> nbdtr_res = nbdtrc(k, n, p) # this will often be faster than below >>> stats_res = nbinom(n, p).sf(k) >>> stats_res, nbdtr_res # test that results are equal (0.6367187499999999, 0.6367187499999999)
nbdtrckann verschiedene Parametersätze auswerten, indem Arrays mit Formen bereitgestellt werden, die für Broadcasting für k, n und p kompatibel sind. Hier berechnen wir die Funktion für drei verschiedene k an vier Orten p, was zu einem 3x4-Array führt.>>> k = np.array([[5], [10], [15]]) >>> p = np.array([0.3, 0.5, 0.7, 0.9]) >>> k.shape, p.shape ((3, 1), (4,))
>>> nbdtrc(k, 5, p) array([[8.49731667e-01, 3.76953125e-01, 4.73489874e-02, 1.46902600e-04], [5.15491059e-01, 5.92346191e-02, 6.72234070e-04, 9.29610100e-09], [2.37507779e-01, 5.90896606e-03, 5.55025308e-06, 3.26346760e-13]])