scipy.special.nbdtrik#

scipy.special.nbdtrik(y, n, p, out=None) = <ufunc 'nbdtrik'>#

Negative binomial Perzentilfunktion.

Gibt das Inverse bezüglich des Parameters k von y = nbdtr(k, n, p), der kumulativen Verteilungsfunktion der negativen Binomialverteilung, zurück.

Parameter:

yarray_like: Die Wahrscheinlichkeit von k oder weniger Misserfolgen vor n Erfolgen (float).
narray_like: Die Zielanzahl von Erfolgen (positive Ganzzahl).
parray_like: Wahrscheinlichkeit eines Erfolgs bei einem einzelnen Ereignis (float).
outndarray, optional: Optionales Ausgabe-Array für die Funktionsergebnisse

Rückgabe:

kSkalar oder ndarray: Die maximal erlaubte Anzahl von Misserfolgen, so dass nbdtr(k, n, p) = y.

Siehe auch

nbdtr: Kumulative Verteilungsfunktion der negativen Binomialverteilung.
nbdtrc: Überlebensfunktion der negativen Binomialverteilung.
nbdtri: Inverses bezüglich p von nbdtr(k, n, p).
nbdtrin: Inverses bezüglich n von nbdtr(k, n, p).
scipy.stats.nbinom: Binomialverteilung (negativ)

Hinweise

Wrapper für die CDFLIB [1] Fortran-Routine cdfnbn.

Formel 26.5.26 aus [2],

\[\sum_{j=k + 1}^\infty {{n + j - 1} \choose{j}} p^n (1 - p)^j = I_{1 - p}(k + 1, n),\]

wird verwendet, um die Berechnung der kumulativen Verteilungsfunktion auf die einer regulierten unvollständigen Betafunktion \(I\) zu reduzieren.

Die Berechnung von k beinhaltet eine Suche nach einem Wert, der den gewünschten Wert von y ergibt. Die Suche beruht auf der Monotonie von y in Bezug auf k.

Referenzen

[1]

Barry Brown, James Lovato, und Kathy Russell, CDFLIB: Library of Fortran Routines for Cumulative Distribution Functions, Inverses, and Other Parameters.

[2]

Milton Abramowitz und Irene A. Stegun, Hrsg. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972.

Beispiele

Berechnen Sie die kumulative Verteilungsfunktion der negativen Binomialverteilung für eine beispielhafte Parameterkombination.

>>> import numpy as np
>>> from scipy.special import nbdtr, nbdtrik
>>> k, n, p = 5, 2, 0.5
>>> cdf_value = nbdtr(k, n, p)
>>> cdf_value
0.9375

Überprüfen Sie, ob nbdtrik den ursprünglichen Wert für k wiederherstellt.

>>> nbdtrik(cdf_value, n, p)
5.0

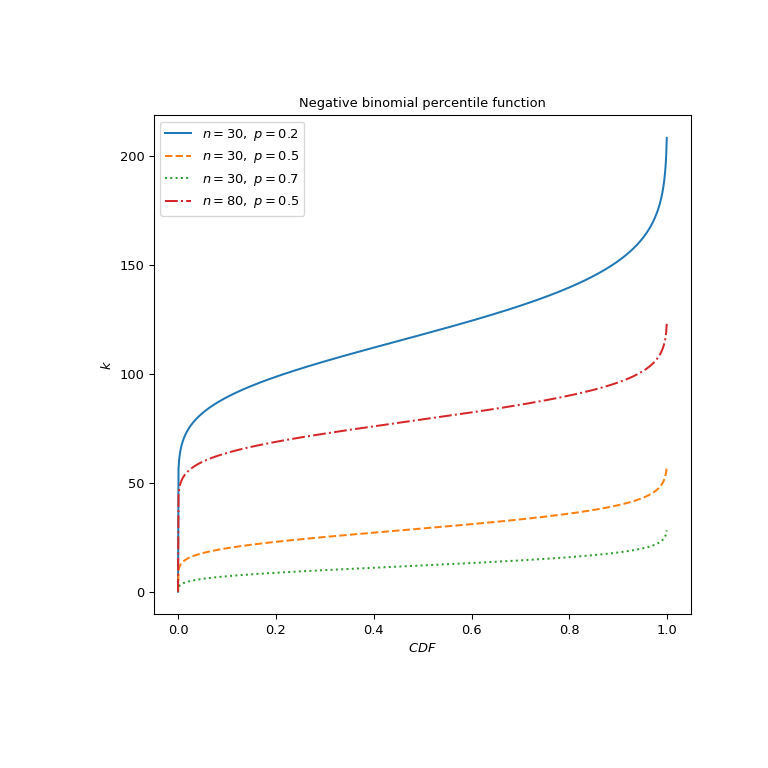
Zeichnen Sie die Funktion für verschiedene Parametersätze.

>>> import matplotlib.pyplot as plt
>>> p_parameters = [0.2, 0.5, 0.7, 0.5]
>>> n_parameters = [30, 30, 30, 80]
>>> linestyles = ['solid', 'dashed', 'dotted', 'dashdot']
>>> parameters_list = list(zip(p_parameters, n_parameters, linestyles))
>>> cdf_vals = np.linspace(0, 1, 1000)
>>> fig, ax = plt.subplots(figsize=(8, 8))
>>> for parameter_set in parameters_list:
...     p, n, style = parameter_set
...     nbdtrik_vals = nbdtrik(cdf_vals, n, p)
...     ax.plot(cdf_vals, nbdtrik_vals, label=rf"$n={n},\ p={p}$",
...             ls=style)
>>> ax.legend()
>>> ax.set_ylabel("$k$")
>>> ax.set_xlabel("$CDF$")
>>> ax.set_title("Negative binomial percentile function")
>>> plt.show()

../../_images/scipy-special-nbdtrik-1_00_00.png

Die negative Binomialverteilung ist auch als scipy.stats.nbinom verfügbar. Die Methode der Perzentilfunktion ppf gibt das Ergebnis von nbdtrik aufgerundet auf ganze Zahlen zurück.

>>> from scipy.stats import nbinom
>>> q, n, p = 0.6, 5, 0.5
>>> nbinom.ppf(q, n, p), nbdtrik(q, n, p)
(5.0, 4.800428460273882)