scipy.special.ncfdtr#

scipy.special.ncfdtr(dfn, dfd, nc, f, out=None) = <ufunc 'ncfdtr'>#

Kumulative Verteilungsfunktion der nicht-zentralen F-Verteilung.

Die nicht-zentrale F-Verteilung beschreibt die Verteilung von,

\[Z = \frac{X/d_n}{Y/d_d}\]

wobei \(X\) und \(Y\) unabhängig verteilt sind, wobei \(X\) nicht-zentral \(\chi^2\) verteilt ist mit dem Nichtzentralitätsparameter nc und \(d_n\) Freiheitsgraden, und \(Y\) \(\chi^2\) verteilt ist mit \(d_d\) Freiheitsgraden.

Parameter:

dfnarray_like: Freiheitsgrade der Zählerquadratsumme. Bereich (0, inf).
dfdarray_like: Freiheitsgrade der Nennerquadratsumme. Bereich (0, inf).
ncarray_like: Nichtzentralitätsparameter. Bereich [0, inf).
farray_like: Quantile, d. h. die obere Integrationsgrenze.
outndarray, optional: Optionales Ausgabe-Array für die Funktionsergebnisse

Rückgabe:

cdfscalar oder ndarray: Die berechnete CDF. Wenn alle Eingaben Skalare sind, ist die Rückgabe ein Float. Andernfalls ist es ein Array.

Siehe auch

ncfdtri: Quantilfunktion; Umkehrung von ncfdtr bezüglich f.
ncfdtridfd: Umkehrung von ncfdtr bezüglich dfd.
ncfdtridfn: Umkehrung von ncfdtr bezüglich dfn.
ncfdtrinc: Umkehrung von ncfdtr bezüglich nc.
scipy.stats.ncf: Nicht-zentrale F-Verteilung.

Hinweise

Diese Funktion berechnet die CDF der nicht-zentralen F-Verteilung unter Verwendung der Boost Math C++-Bibliothek [1].

Die kumulative Verteilungsfunktion wird nach Formel 26.6.20 von [2] berechnet

\[F(d_n, d_d, n_c, f) = \sum_{j=0}^\infty e^{-n_c/2} \frac{(n_c/2)^j}{j!} I_{x}(\frac{d_n}{2} + j, \frac{d_d}{2}),\]

wobei \(I\) die regularisierte unvollständige Betafunktion ist und \(x = f d_n/(f d_n + d_d)\).

Beachten Sie, dass die Argumentreihenfolge von ncfdtr von der der ähnlichen cdf-Methode von scipy.stats.ncf abweicht: f ist der letzte Parameter von ncfdtr, aber der erste Parameter von scipy.stats.ncf.cdf.

Referenzen

[1]

The Boost Developers. “Boost C++ Libraries”. https://www.boost.org/.

[2]

Milton Abramowitz und Irene A. Stegun, Hrsg. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972.

Beispiele

>>> import numpy as np
>>> from scipy import special
>>> from scipy import stats
>>> import matplotlib.pyplot as plt

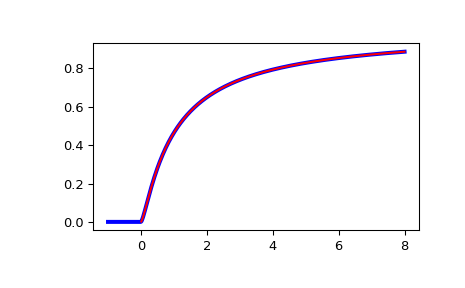
Plot der CDF der nicht-zentralen F-Verteilung für nc=0. Vergleich mit der F-Verteilung aus scipy.stats

>>> x = np.linspace(-1, 8, num=500)
>>> dfn = 3
>>> dfd = 2
>>> ncf_stats = stats.f.cdf(x, dfn, dfd)
>>> ncf_special = special.ncfdtr(dfn, dfd, 0, x)

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.plot(x, ncf_stats, 'b-', lw=3)
>>> ax.plot(x, ncf_special, 'r-')
>>> plt.show()

../../_images/scipy-special-ncfdtr-1.png